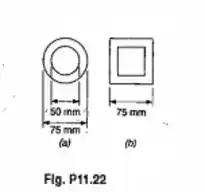
Duas barras de latão usadas como membros em compressão, cada uma delas com 1,8m de comprimento efetivo, tem as seções transversais mostradas. Determinar. (a) a espessura da parede da barra vazada quadrada, para que as barras tenham a mesma área da seção transversal;(b) a carga crítica para cada barra, usando E=105GPa

Como o enunciado nos definiu que as áreas são iguais, vamos calcular a área da seção redonda e depois comparar com a quadrada.

Substituindo temos:

Agora vamos analisar a seção quadrada, uma área de seção quadrada vazada é dada por:

Onde é a aresta e é a espessura.

Igualando as áreas como diz o enunciado a gente tem:

E substituindo

Rearrumando isso a gente fica com:

Extraindo as raízes temos:

Isolando t, temos o item a.

Pro item b não tem mistério é calcular a carga crítica de ambas, primeiro temos que calcular os momentos de inércia, para a seção redonda temos:

E para a seção quadrada:

Daí:

Agora usando a fórmula do peso crítico para a coluna redonda temos:

Substituindo:

E para a coluna quadrada:

E substituindo:

Detalhe que aqui trabalhamos com todas as medidas em milímetros e o módulo de elasticidade em gigapascal e nossos resultados saem em kilonewtons.