Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 116

116- Resolva o Problema 6.114 considerando que a força P é substituída por um binário no sentido horário de momento M 0 aplicado ao elemento C D E em D .

Passo 1

Desenhando as forças nas barras nesse novo caso nós teremos:

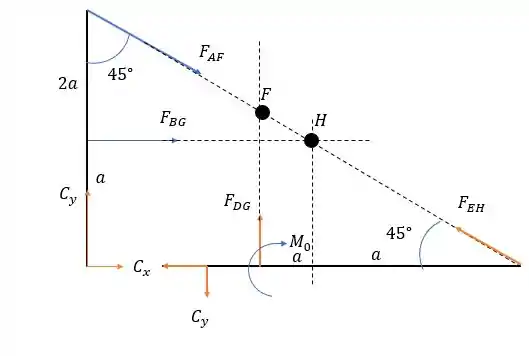
Na barra A B C vamos fazer a somatória dos momentos H .

- 2 C y a + C x a = 0

C x = 2 C y   ( 1 )

Agora a somatória dos momentos em F na barra C D E .

- M 0 - 2 a C x + C y a = 0

C y - 2 C x = M 0 a   ( 2 )

Porém se aplicarmos ( 1 ) em ( 2 ) nós teremos:

C y - 4 C y = M 0 a

- 3 C y = M 0 a

C y = - M 0 3 a

Logo pela equação ( 1 ) :

C x = - 2 M 0 3 a

Passo 2

Fazendo a somatória das forças na barra C D E nós temos:

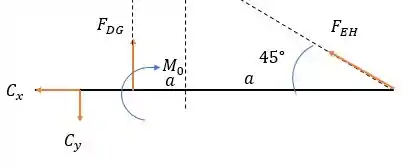
Forças horizontais:

C x + F E H cos ⁡ 45 = 0

F E H = - C x cos ⁡ 45 = 2 M 0 3 a 2 2 = 2 M 0 3 a   2 = 2 2 M 0 3 a

Força de tração.

Agora fazendo a somatória das forças verticais:

C y = F D G + F E H sin ⁡ 45

F D G = C y - F E H sin ⁡ 45

F D G = - M 0 3 a - 2 2 M 0 3 a 2 2 = - M 0 3 a - 2 M 0 3 a = - M 0 a

Força de compressão.

Passo 3

Pelas forças na barra A B C temos:

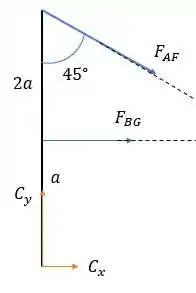
Pela somatória das forças verticais:

C y = F A F cos ⁡ 45

F A F = C y cos ⁡ 45 = - M 0 3 a 2 2 = - 2 M 0 3 2 a = - M 0 2 3 a

Força de compressão.

Agora pela somatória das forças horizontais:

C x + F B G + F A F sin ⁡ 45 = 0

F B G = - C x - F A F sin ⁡ 45

F B G = 2 M 0 3 a + M 0 2 3 a 2 2 = 2 M 0 3 a + M 0 3 = M 0 a

Força de tração.

Resposta

F E H = 2 2 M 0 3   ( T )

F D G = - M 0 a   ( C )

F A F = M 0 2 3 a   ( C )

F B G = M 0 a   ( T )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

103- Sabendo que P = 65N e Q = 290N , determine os componentes das forças exercidas a ) no elemento B C D F em C e D , b ) no elemento A C E G em E .
101- Para a estrutura e carregamento mostrados na figura, determine os componentes de todas as forças atuantes no elemento A B E .
108- O eixo do carco de três articulações A B C é uma parábola com vértice em B . Sabendo que P = 140k N e Q = 112k N , determine a ) os componentes da reação em A , b ) os componentes da força exerci
107- O eixo do arco de três articulações A B C é uma parábola com vértice em B . Sabendo que P = 112k N e Q = 140k N , determine a ) os componentes da reação em A , b ) os componentes da força exercid
106- Resolva o Problema 6.105 considerando que a carga de 6k N foi removida.