A treliça mostrada na figura consiste em seis elementos e é sustentada por uma pequena haste de conexão em A, duas pequenas hastes de conexão em B e por uma rótula em D. Determine a força em cada um dos elementos para o carregamento dado.
Passo 1
Tá legal! Vamos começar o exercício desenhando o diagrama de corpo livre da treliça:
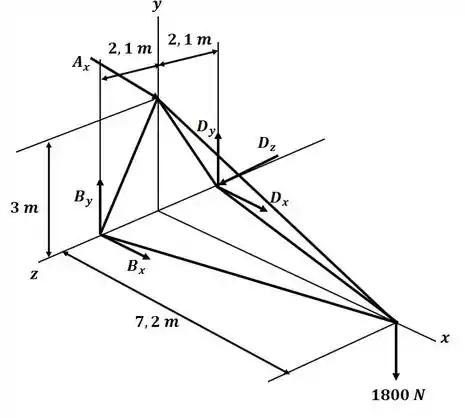
Devido a simetria da treliça e do carregamento, que se encontra na ponta da treliça e sobre o eixo central, sabemos que:
Então, vamos começar aplicando o somatório de momento com relação ao eixo :
Agora, aplicando o somatório de forças na direção :
Como sabemos que , podemos substituir esse valor na equação anterior, obtendo:
E, agora fazendo o somatório de forças na direção :
Passo 2
Agora vamos analisar o nó C:

Nesse caso, devemos calcular as direções das três forças desconhecidas. Podemos escrever as forças em função de seu módulo e de suas componentes direcionais da seguinte forma:
Onde é o módulo da força, é o segmento de reta ligando os dois pontos e é o módulo desse comprimento, então, com os valores obtidos da figura do enunciado, temos:
E, seu módulo será:
Fazendo o mesmo procedimento para e :
E, seu módulo será:
E, para :
E, seu módulo será:
Então, reescrevendo as forças, temos:
Passo 3
Agora podemos aplicar o somatório de forças para o nó, de forma que:
Então, abrindo as equações em suas componentes:
Então, da segunda equação, temos:
Da terceira equação:
Substituindo esses dois últimos resultados na primeira equação, temos:
E, substituindo esse valor na terceira equação:
Passo 4
Agora vamos analisar o nó B:
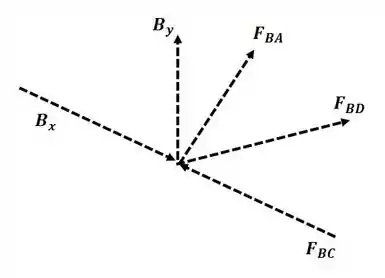
Agora vamos calcular as forças novamente pelo mesmo método, então para :
Para :
E, para :
Então, aplicando o somatório de forças para o nó B:
Separando em componentes:
E, devido a simetria em :