Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 47
47. Determine a força nos membros e da treliça e indique se os membros estão sob tração ou compressão. Além disso, indique todos os membros de força zero.
Passo 1
Primeiro vamos achar os membros de força zero pois são relativamente mais fáceis.
Em geral se três membros formam um nó da treliça onde dois dos membros são colineares, o terceiro membro é um membro de força zero.
Sabendo disso, podemos ver que os membros de força zero são:
Isso também pode ser verificado se você fazer a verificação das equações de equilíbrio nos pontos .
Para começar a resolver a outra parte do problema, primeiro vamos analisar o digrama de corpo livre a seguir:
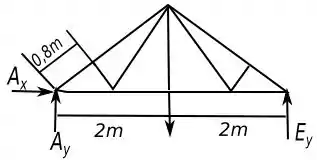
Observando o digrama, vemos que será necessário determinar, já que ele influencia os membros que queremos determinar e vamos fazer isso através das equações de equilíbrio do momento no ponto , pois assim e não contribuem para essa conta.
Tendo isso vamos fazer um corte que passa pelos membros e , para nos facilitar a análise e assim descobrir o valor das forças através das equações de equilíbrio.
Inicialmente vamos considerar todas as forças como sendo de tração, caso alguma apareça de forma negativa, saberemos que ela não é de tração, mas sim de compressão.
Passo 2
Vamos determinar :
Passo 3
Agora vamos analisar o digrama de corpo livre da seção que sofreu o corte mencionado no passo 1.
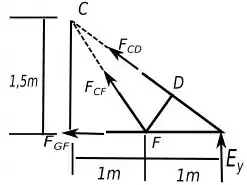
Olhando o diagrama é possível perceber que precisaremos das componentes da força para podermos usar as equações de equilíbrio. Para isso, temos que achar o ângulo que essa força faz com a horizontal para aí sim decompô-la.
Para achar esse ângulo podemos usar uma trigonometria simples já que essa força faz parte de um triângulo.
Temos que para :
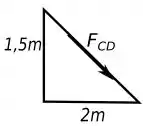
Passo 4
Agora vamos aplicar as equações de equilíbrio.
Vamos começar com o ponto , já que não contribui para o momento em .
Então:
Como o resultado foi negativo, essa força não é uma força de tração, mas sim de compressão.
Passo 5
Agora vamos analisar o ponto para encontrarmos .
Como o resultado foi positivo, essa força é realmente uma força de tração.