Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 122
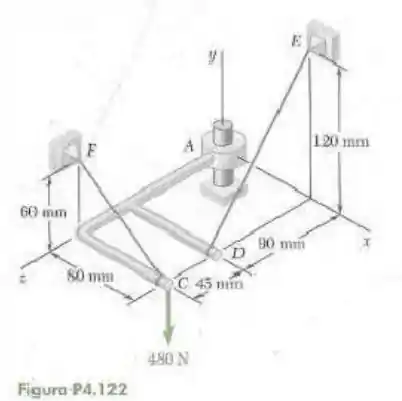
122- O conjunto mostrado na figura é soldado ao cursor , que se encaixa no pino vertical mostrado. O pino pode exercer binários em torno dos eixos e , mas não impede movimento em torno ou ao longo do eixo . Para o carregamento mostrado, determine a tração em cada cabo e a reação em .
Passo 1
Em teremos reações e e momentos de reação iguais a e . Para calcular o momento em precisaremos vetorizar a força nos cabos e para isso vamos considerar um força indo de até e outra indo de até e então teremos:
Considerando as forças saindo de e de então precisamos conhecer as distâncias relativas desses pontos em relação a .
Em temos também a força de .
Passo 2
Agora a somatória dos momentos em será igual a:
Fazendo esses determinantes nós temos:
Isso nos dará o seguinte sistema para resolver:
Nós temos 3 equações para incógnitas. Não conseguimos resolver! Porém vamos resolver a somatória das forças no sistema pois em não teremos nenhuma influência de nela:
Essa equação com a segunda nos dá o seguinte sistema:
E que nos dará os seguintes valores:
O que responde a primeira pergunta.
Passo 3
Agora vamos substituir os valores de e para encontrar o vetor do momento em :
Logo o valor do momento em será:
Passo 4
Agora vamos somar as forças em e em para encontrar as reações em :
O que nos dá um vetor de reação em igual a: