Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 123
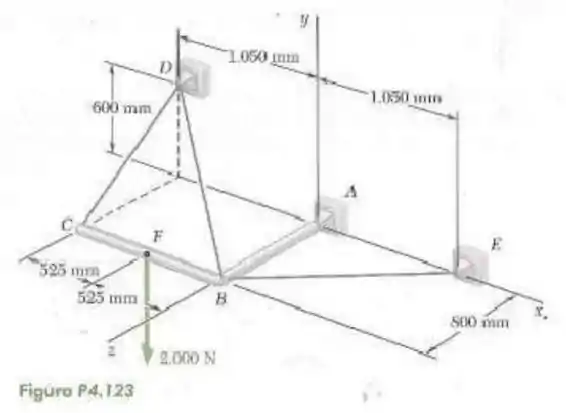
123- O elemento rígido em formato de é sustentado por uma rótula em e por três cabos. Se um carregamento de é aplicado em , determine a tração em cada cabo.
Passo 1
Primeiramente vamos vetorizar as forças em cada cabo.
Considerando que duas forças saem de teremos:
Agora falta a força que vamos considerar saindo de e indo até .
Passo 2
Como vamos fazer a somatória dos momentos em vamos calcular a distância relativa desse ponto até e e em (que tem reação a força nos três sentidos). Pois e não fazem momento em
Então o somatório dos momentos em dará:
O determinante dessas matrizes nos dará:
O que nos dá 3 equações para quatro incógnitas. Porém vamos utilizar a somatória das forças para conseguirmos resolver isso.
Por essas duas equações temos que:
Passo 3
Pela somatória das forças temos:
Isso nos dará:
Dessa última relação encontramos que:
Então da última equação escrita do passo 2 temos:
Então pela primeira equação desse sistema (nesse passo) teremos:
Isso nos dará: