Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 112
112- Resolva o Problema , supondo que a força de é apontada para a direita.
Passo 1
A diferença da questão passada é que:
A somatória das forças verticais é:
E a somatória das forças horizontais será:
Com:
Isso faz com que a força resultante seja:
E o ângulo formado com a horizontal será:
Vetor apontado para a diagonal superior direita, pois a força resultante em e em são positivas.
Passo 2
E a somatória dos momentos em será:
O que nos dá:
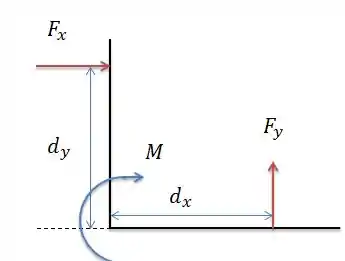
Porém não da para encontrar a distancia vertical de pois :
O que nos daria uma distância para baixo, o que não pode pois sai da forma da placa.
Passo 3
O que fazer? Vamos considerar que a barra está no mesmo nível que o plano e com isso calcular o momento em utilizando a força vertical da seguinte forma:
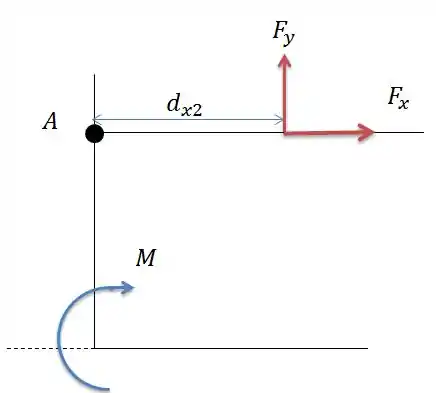
A somatória dos momentos em nos dá:
Então a forca resultante também está a de , isso é só porque não podemos calcular a posição em relação a uma das forças.