Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 60

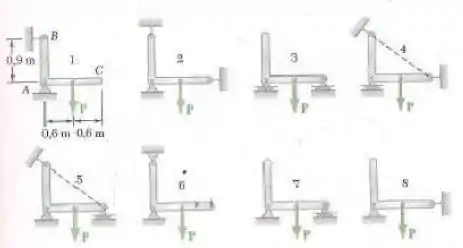
O suporte pode ser apoiado das oito diferentes maneiras mostradas nas figuras. Todas as conexões consistem em pinos sem atrito, roletes ou hastes curtas. Em cada caso, responda às questões apresentadas no Problema e, onde for possível, calcule as reações, considerando que a força é .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para esta questão, iremos analisar cada suporte podendo ser apoiado de oito maneiras como mostrado na figura.

Analisando o diagrama de corpo livre do primeiro suporte, temos que:

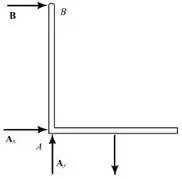
Existem 3 vetores não concorrentes com reações não paralelas:

O suporte está com restrição completa.
As reações são estaticamente determinadas
O equilíbrio do suporte é mantido.

Passo 2

Vamos analisar o somatório de momentos de , para calcularmos as reações:

Fazendo o somatório de forças em , temos:

Usando teorema de Pitágoras para achar o valor da reação no ponto , temos:

Com ângulo de:

Logo:

Passo 3

Analisando o diagrama de corpo livre do segundo suporte, temos que:

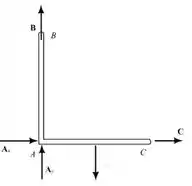
Existem 4 vetores concorrentes:

O suporte está impropriamente vinculado.
As reações são estaticamente indeterminadas
O equilíbrio do suporte não é mantido.

Portanto, não é possível calcular as reações.

Passo 4

Analisando o diagrama de corpo livre do terceiro suporte, temos que:

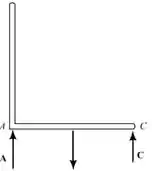
Existem 3 reações paralelas:

O suporte está parcialmente vinculado.
As reações são estaticamente determinadas
O equilíbrio do suporte é mantido.

Passo 5

Vamos analisar o somatório de momentos de , para calcularmos as reações:

Fazendo o somatório de forças em , temos:

Passo 6

Analisando o diagrama de corpo livre do quarto suporte, temos que:

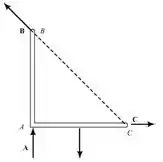
Existem 3 reações não simultâneas e não paralelas:

O suporte está completamente restrito.
As reações são estaticamente determinadas
O equilíbrio do suporte é mantido.

Passo 7

Portanto, vamos encontrar o ângulo através da análise geométrica:

Vamos analisar o somatório de momentos de , para calcularmos as reações:

Fazendo o somatório de forças em , temos:

Passo 8

Analisando o diagrama de corpo livre do quinto suporte, temos que:

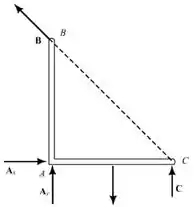
Existem reações não simultâneas e não paralelas:

O suporte está completamente restrito.
As reações são estaticamente indeterminadas
O equilíbrio do suporte é mantido.

Passo 9

Analisando o diagrama de corpo livre do sexto suporte, temos que:

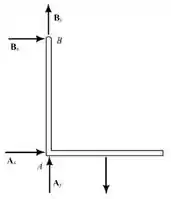
Existem reações não simultâneas e não paralelas:

O suporte está completamente restrito.
As reações são estaticamente indeterminadas
O equilíbrio do suporte é mantido.

Passo 10

Vamos analisar o somatório de momentos de , para calcularmos as reações:

Fazendo o somatório de forças em , temos:

Passo 11

Analisando o diagrama de corpo livre do sétimo suporte, temos que:

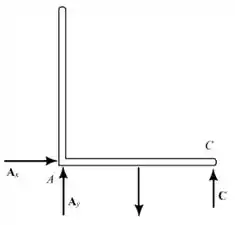
Existem reações não simultâneas e não paralelas:

O suporte está completamente restrito.
As reações são estaticamente determinadas
O equilíbrio do suporte é mantido.

Passo 12

Vamos analisar o somatório de momentos de , para calcularmos as reações:

Fazendo o somatório de forças em , temos:

Passo 13

Analisando o diagrama de corpo livre do oitavo suporte, temos que:

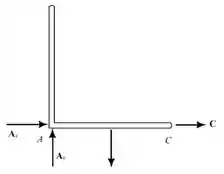
Existem reações não simultâneas e não paralelas:

O suporte está impropriamente restrito.
As reações são estaticamente indeterminadas
O equilíbrio do suporte não é mantido.

Resposta

Suporte 1:

O suporte está com restrição completa.
As reações são estaticamente determinadas
O equilíbrio do suporte é mantido.

Suporte 2:

O suporte está impropriamente vinculado.
As reações são estaticamente indeterminadas
O equilíbrio do suporte não é mantido.

Suporte 3:

O suporte está parcialmente vinculado.
As reações são estaticamente determinadas
O equilíbrio do suporte é mantido.

Suporte 4:

O suporte está completamente restrito.
As reações são estaticamente determinadas
O equilíbrio do suporte é mantido.

Suporte 5:

O suporte está completamente restrito.
As reações são estaticamente indeterminadas
O equilíbrio do suporte é mantido.

Suporte 6:

O suporte está completamente restrito.
As reações são estaticamente indeterminadas
O equilíbrio do suporte é mantido.

Suporte 7:

O suporte está completamente restrito.
As reações são estaticamente determinadas
O equilíbrio do suporte é mantido.

Suporte 8:

O suporte está impropriamente restrito.
As reações são estaticamente indeterminadas
O equilíbrio do suporte não é mantido.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.33. A grua é sustentada por um pino em C e um cabo AB. O cabo pode suportar uma tração máxima de 40k N . Se uma carga possui uma massa de 2M g com seu centro de massa localizado em G, determine sua

5.29. A massa de 700k g é suspensa por um gancho que se move ao longo de um trilho d = 1,7m até d = 3,5m . Determine a força ao longo da cantoneira conectada por pino BC (ligação curta) e a intensidad

5.39. A mola CD permanece na posição horizontal o tempo todo devido ao rodízio em D. Se a mola está descarregada quando θ = 0 e a rigidez é k = 1,5 k N m , determine o menor ângulo θ para o equilíbrio

5.52. Três livros uniformes, cada um com peso W e comprimento a , são empilhados como na figura. Determine a distância máxima d que o livro do topo pode se projetar em relação ao da base, de modo que

5.43. A barra uniforme AB possui peso de 75N . Determine a força no cabo quando a barra está na posição mostrada.