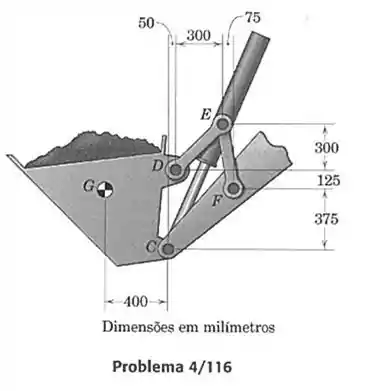
116- Considere o detalhe dimensional adicional para o sistema do Prob. 4/115. Determine a força no cilindro hidráulico . A massa da caçamba e de sua carga é de , com centro de massa em . Você pode desprezar os efeitos dos pesos dos outros elementos.
Passo 1
O sistema pode ser desenhado da seguinte forma:
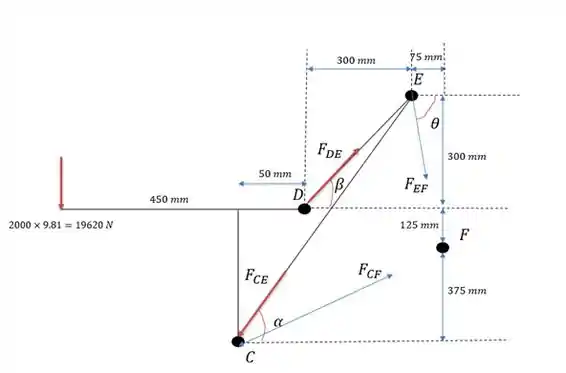
Onde é:
E é:
E :
Passo 2
Como temos a existência de duas forças no ponto e como só temos uma força no ponto primeiramente vamos fazer a somatória dos momentos em .
Onde considerei o sentido horário como positivo:
Isso nos dá:
Passo 3
Agora podemos analisar o nó para encontrar a força no cilindro , o que nos dá a figura.
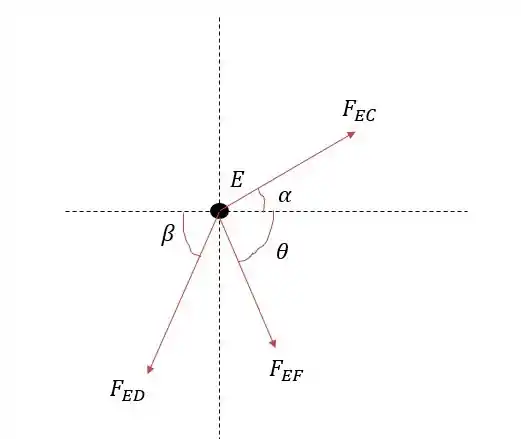
Fazendo a somatória das forças verticais e igualando –as a zero teremos:
E para as forças horizontais:
O que nos dá o sistema:
Resolvendo encontramos:
Logo a força feita pelo cilindro será de .