Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 73
Determine a reação no rolete para o suporte carregado mostrado
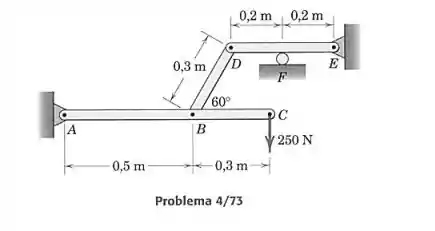
Passo 1
Vamos encontrar a reação fazendo o diagrama de corpo livre para cada corpo e resolvendo as equações de equilíbrio, prestando atenção às forças de ação e reação entre os corpos. Não precisamos representar pois é um elemento de duas forças, ou seja, tem uma força em cada ponta de mesmo módulo, com mesma direção e sentidos contrários. Vamos desconsiderar os pinos, fazendo como se as barras fizessem força diretamente umas nas outras. Vamos representar as barras e :
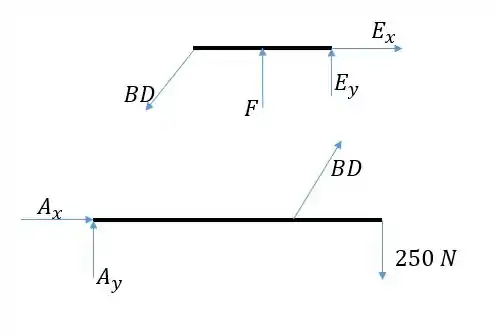
Passo 2
Temos para a barra 4 forças desconhecidas, então não conseguimos resolver as equações só com essa barra. Precisamos achar a força através da outra barra. Achamos ela diretamente calculando o momento em torno de , pois evitamos as forças desconhecidas nesse ponto e trabalhamos apenas com como incógnita. Então:
Agora indo para a outra barra, vemos que se fizermos o momento em torno de só teremos como incógnitas (que já foi encontrado) e que queremos achar:
Substituindo o valor de já encontrado e o seno: