Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 122
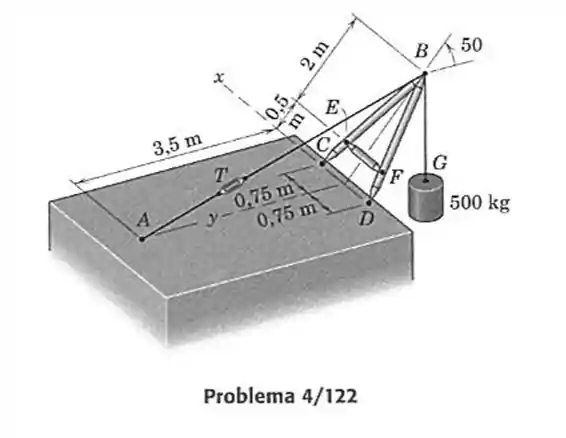
122- Na representação esquemática de uma estrutura real, representa um parafuso de aperto, e são dobradiças cujos eixos estão ao longo da linha e , e são rótulas. Determine a força de tração no parafuso e a força no elemento .
Passo 1
Vamos observar a estrutura de lado e traçar o diagrama de forças.
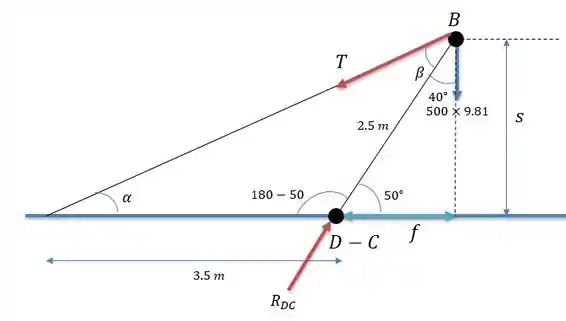
Precisamos calcular os valores de ângulos dentro desse triângulo.
Para calcular vamos fazer:
Onde se calcula da seguinte maneira:
E utiliza o mesmo triângulo retângulo.
Logo será:
Agora o valor de será:
Passo 2
Agora podemos encontrar a força de tração ao fazer a somatória dos momentos em , porém para isso precisaremos calcular um eixo normal a esse ponto para poder calcular o momento no ponto.
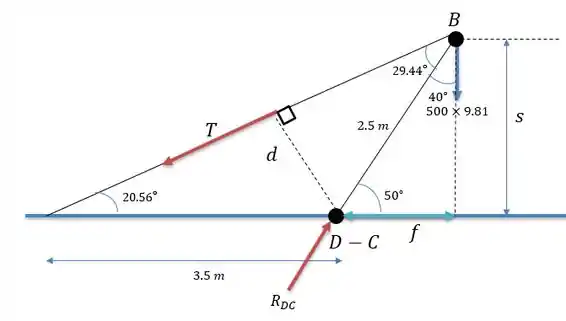
O valor de pode ser calculado fazendo:
Logo o valor de valerá (pela somatória dos momentos em ser zero):
Agora fazendo a somatória das forças ser zero nós conseguiremos encontrar o valor de :
Passo 3
Agora podemos encontrar a força no elemento para isso precisamos entender que nos pontos e temos a reação que equivale a metade da reação logo:
Uma vez que essa força é dividida entre as duas barras. Logo pegando somente a barra teremos:
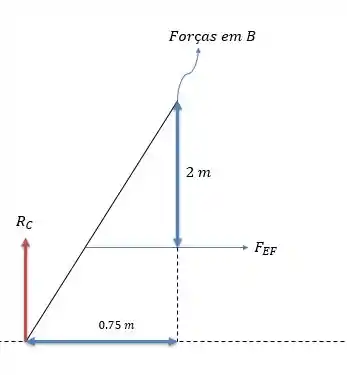
Fazendo a somatória dos momentos em nós temos: