Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 47
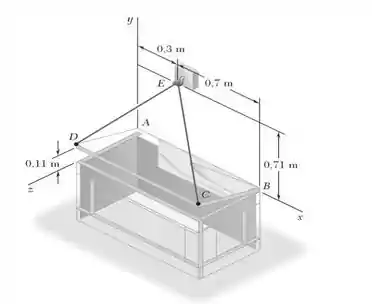
47. A tampa de uma caixa de engrenagem de , é articulada ao longo do lado e mantida aberta com uma corda lançada sem atrito a um gancho em . Sabendo-se que a tração na corda é , determine o momento em relação a cada um dos eixos de coordenadas da força exercida pelo corda em .
Passo 1
Bom! Para fazer o nosso cálculo, nos precisamos da distância ; não é mesmo? Mas repara que aquele ponto não está exatamente posicionado numa linha horizontal e paralela ao eixo . Ele está um pouco inclinado pra cima. Ou seja, o que se quis dizer com todo essa lenga-lenga é que precisamos calcular a coordenada em do ponto . A figura abaixo demonstra isso:
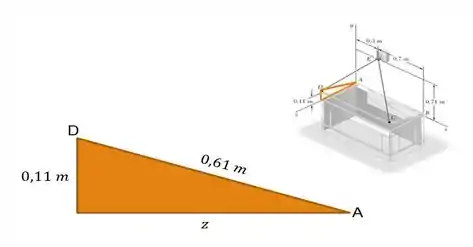
Só que pra nossa sorte, precisamos apenas usar Pitágoras para calcular nossa coodernada :
E para calcular a distância basta calcular a raiz quadrada abaixo:
Onde para o ponto temos que:
E para o ponto temos:
Obtidas as nossas coordenadas; façamos o cálculo:
Passo 2
Obtida a nossa distância vamos obter o quanto vale a força de tração em termos dos vetores unitários e . Para fazer isso basta multiplicar a força pela distância vetorial e dividir tudo pelo módulo de , que já encontramos no :
E como temos que ; basta fazer o seguinte cálculo agora:
Passo 3
A questão nos pede para determinar o momento em relação a cada um dos eixos de coordenadas da força exercida pelo corda em . Ora bolas; já temos a nossa força de tração !!! O que precisamos mais??
Bom! Só falta agora, o vetor posição que parte da origem até a linha de ação da força em . Essa belezinha é o vetor ; que podemos calcular apenas determinando as coordenadas do ponto ; já que é o ponto origem do nosso referencial. Bora por a mão na massa:
Como temos tudo que precisamos; só nos resta aplicar a definição de momento:
Onde temos que:
Vamos então, fazer o produto vetorial acima usando o determinante matricial:
Esse é o nosso momento resultante!!! Para obter os momentos em cada eixo; basta associar cada componente de momento com seu versor ao respectivo eixo coordenado; para o eixo ; para o eixo e para o eixo :