Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 105
105- Para a estrutura e carregamento mostrado na figura, determine os componentes das forças atuantes no elementos em e .
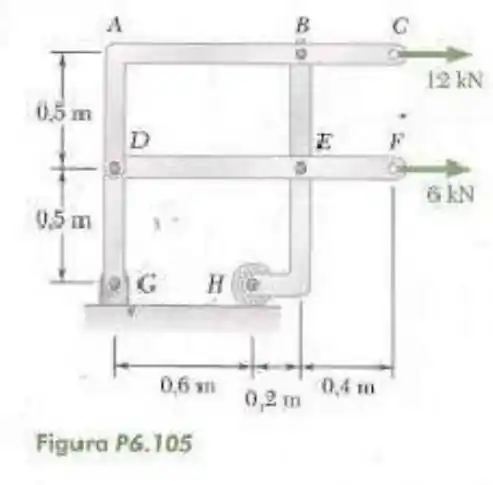
Passo 1
Encontrando as forças em e analisando a força de corpo inteiro temos:
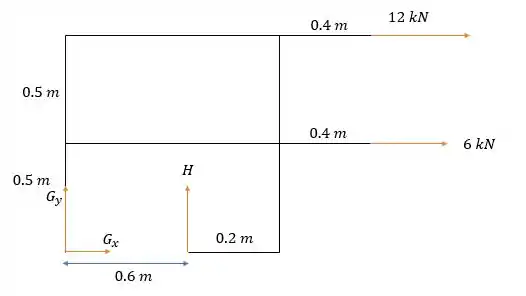
Pela somatória das forças verticais temos que:
E pela somatória das forças horizontais:
E a somatória dos momentos em nos dão:
Logo e aponta para a esquerda.
Passo 2
Por ter um pino somente vamos para a barra .
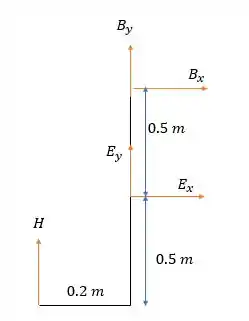
Fazendo a somatória dos momentos em temos:
Apontando para a esquerda nessa barra, mas apontando para a direita em por ação e reação.
Passo 3
Agora podemos ir para a barra .
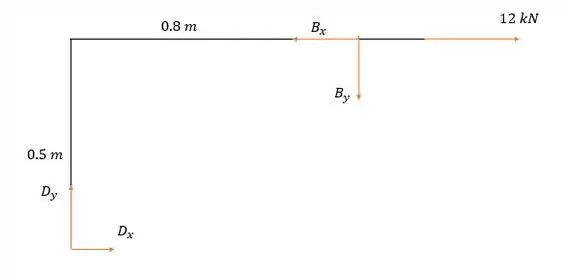
Fazendo a somatória das forças horizontais temos:
Força que vai apontar para a esquerda.
Agora a somatória dos momentos em será:
Força que terá sentido para baixo.
Com isso pela soma das forças verticais temos:
Força que irá apontar para cima.
Em todos as forças o sinal se mantém, mas o sentido do vetor muda de estrutura para outra.