Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 107
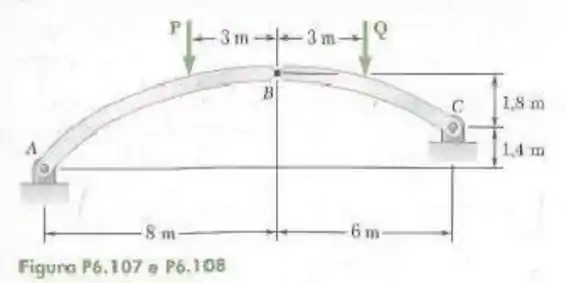
107- O eixo do arco de três articulações é uma parábola com vértice em . Sabendo que e , determine os componentes da reação em , os componentes da força exercida em sobre o segmento .
Passo 1
Vamos fazer esse exercício teoricamente pois a próxima é a mesma coisa somente muda os valores.
Dividindo o eixo em teremos a seguinte decomposição de forças.
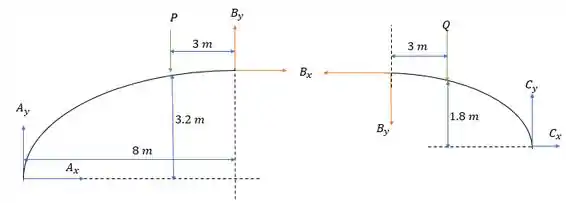
Pela estrutura a esquerda temos que a soma das forças horizontais nos dará:
E a soma das forças verticais:
Agora fazendo a somatória dos momentos em teremos:
Dessa forma:
Passo 2
Se olharmos para a estrutura toda temos que:
E
E a somatória dos momentos em nos dará:
Passo 3
Agora olhando para a estrutura a direita temos:
E pela somatória dos momentos em .
Fazendo um sistema de com temos:
Multiplicando a primeira por e a segunda por teremos”
Somando:
Dessa forma será:
O que fica:
Não esquecendo que temos:
E
Passo 4
Aplicando os valores de e temos:
b)
Sentido para a esquerda em
Sentido para baixo em
a)
Sentido para a direita
Sentido para cima em .