Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 117
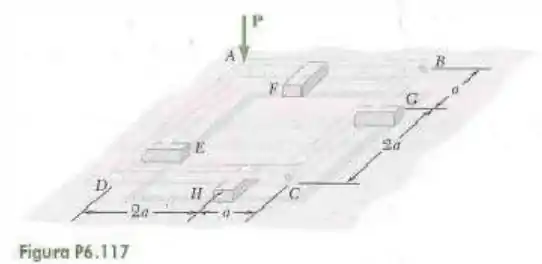
117- Quatro vigas, cada qual de comprimento , são pregadas juntas com um único prego em e . Cada viga é fixada a um suporte localizado a uma distância a partir da ponta da viga como mostrado na figura. Considerando que apenas forças verticais são exercidas nas conexões, determine as reações verticais em e .
Passo 1
Não sei se deu para entender o desenho, mas temos uma armação quadrada onde e tem pregos, logo temos ação e reação. Supondo que a força está agindo na viga nós teremos as seguintes reações em todas as vigas.
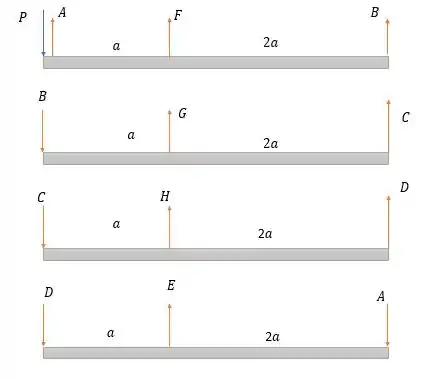
Fazendo a somatória dos momentos em e temos:
Como somente há forças verticais nas conexões, então somente vamos representar as forças verticais nos pregos
Passo 2
Organizando nós temos:
Aí basicamente, nós queremos organizar todas as forças em função de .
Porém podemos escrever tudo em função de ficando:
Isso dá:
Passo 3
Agora fazendo somatória das forças em todas as vigas nós vamos ter:
Isso nos dá:
Sentido para cima.
Sentido para baixo.
Sentido para cima.
Sentido para baixo.