Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 120

120- A figura mostra um dispositivo especial, projetado para levantar seções verticais de uma torre de construção. O conjunto A tem uma massa de 1.5   M g e é erguido pela plataforma B , que tem uma massa de 2   M g . A plataforma sobe pela coluna vertical fixa sobre roletes e é ativada pelo cilindro hidráulico C D e pelas conexões E D F e F H . Para a posição particular mostrada, calcule a força R exercida pelo cilindro hidráulico em D e o módulo da força suportada pelo pino em E .

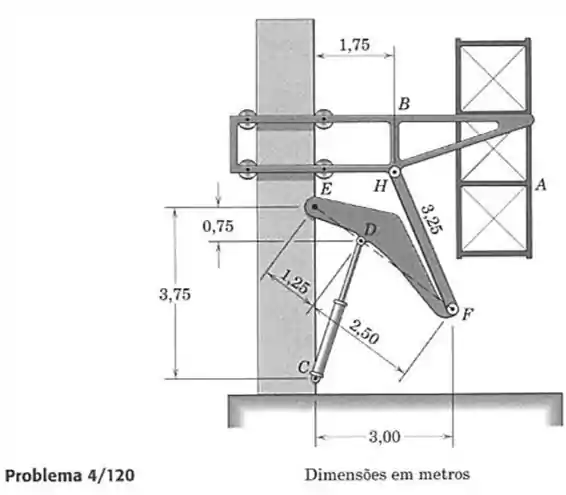
Passo 1

Um diagrama otimizado e com os ângulos que mais nos interessam é a melhor saída para solucionar esse tipo de problema.

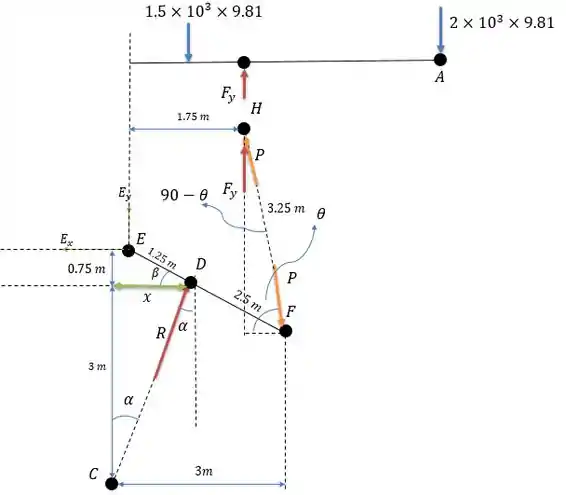
Bastante coisa né? Mas calma, primeiro vamos localizar os ângulos , o primeiro podendo ser β .

sin ⁡ β = 0.75 1.25 → β = 36.87

Onde x nesse mesmo triângulo vale:

1.25 2 = 0.75 2 + x 2 → x = 1

Logo α valerá:

t g   α = 1 3 → α = 18.435

Para o valor de θ devemos ver que o seu cateto adjacente vale 3 - 1.75 = 1.25   m . Logo:

cos ⁡ θ = 1.25 3.25 → θ = 67.38

E que o valor de F y será:

F y = P c o s   90 - 67.38 = P c o s ( 22.62 )

Passo 2

Agora podemos encontrar o valor de P simplesmente fazendo a somatória das forças verticais presentes na plataforma, já que a força empregada no ponto B será transferida para o ponto H .

1.5 + 2 × 10 3 × 9.81 = P c o s   22.62

P = 37.2   k N

Passo 3

Agora para encontrar a força R vamos fazer a somatória dos momentos em E no elemento E D F . Para isso precisamos projetar a barra e as forças em x e y .

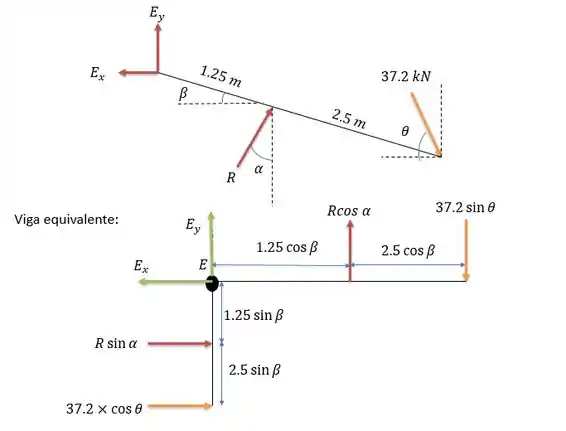
Considerando o sentido anti- horário como positivo temos:

37.2 cos ⁡ θ 3.75   s i n β + R s i n   α ( 1.25 sin ⁡ β ) + R c o s   α ( 1.25 cos ⁡ β ) - 37.2 sin ⁡ θ ( 3.75 cos ⁡ β ) = 0

R ( 1.25 sin ⁡ β sin ⁡ α + 1.25 cos ⁡ α cos ⁡ β ) = - 139.5 ( s i n β + cos ⁡ β )

R = - 111.6 ( cos θsin ⁡ β - sin θcos ⁡ β ) s i n β s i n α + cos ⁡ α cos ⁡ β

Substituindo os valores de α , β e θ , encontramos.

R = 59.72   k N

Passo 4

Agora vamos encontrar as reações em E fazendo a somatória das forças verticais e horizontais.

∑ F y = 0

E y = R c o s   α - 37.2 sin ⁡ θ

Substituindo os valores:

E y = 59.72 × cos ⁡ 18.435 - 37.2 × sin ⁡ 67.38 = 22.32   k N

Fazendo a somatória das forças horizontais:

E x = R s i n   α + 37.2 × c o s θ

Substituindo:

E x = 59.72 × sin ⁡ 18.435 + 37.2 × cos ⁡ 67.38 = 33.2   k N

Agora a força E será:

E = E x 2 + E y 2 = 33.2 2 + 22.32 2 = 40   k N

Resposta

R = 59.72   k N

E = 40   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

135. A placa A B C D de 50k g é sustentada por dobradiças ao longo de A B e pelo arame C E . Sabendo que a placa é uniforme, determine a tração no arame.
133. A haste dobrada A B D E é apoiada por rótulas em A e E e pelo cabo D F . Se uma carga de 240N é aplicada em C , tal como mostra a figura, determine a tração no cabo.
131. A montagem mostrada na figura consiste em uma barra A F de 80m m que é soldada a uma cruz representada por quatro braços de 200m m . A montagem é mantida por uma rótula em F e por três conexões c
136. Resolva o Problema 4.135 , considerando que o arame C E é substituído por um arame que conecte E e D .
139. Resolva o Problema 4.138 , sujeito à restrição de que H deve estar sobre o eixo y .