Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 246
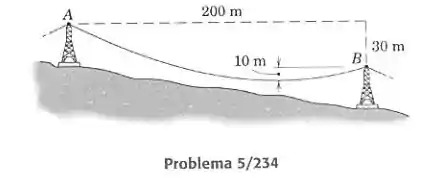
Um determinado comprimento de um cabo de transmissão está suspenso das duas torres, como mostrado. O cabo tem uma massa de 20 kg por metro. Se a máxima força trativa admissível no cabo vale 75 kN, determine a massa de gelo por metro de cabo, que pode se formar sobre o cabo sem que a máxima força trativa admissível se seja excedida. Se o alongamento adicional no cabo for desprezado, a presença do gelo muda a configuração do cabo?
Passo 1
Para esse problema primeiro devemos perceber que esse cabo está sob efeito apenas da força peso, que age em cada elemento dependendo do comprimento desse elemento, e da tração. Esse é então um cabo catenário, e tem o formato dado pela seguinte equação:
Escolhendo como origem o ponto mais baixo, temos o ponto pertencendo à curva, então:
Sendo a tração horizontal no ponto mais baixo da corda e a intensidade da força por metro da corda. Outra equação dada pelo livro relaciona a tração em qualquer ponto da corda de coordenada com a tração que age no ponto mais baixo:
Devemos descobrir o ponto de tração máxima da corda, e então aplicar o caso limite onde a tração nesse ponto é igual à máxima admissível pelo cabo. Com isso iremos aplicar a eq. (2) e encontrar , a intensidade de força atuante na corda por comprimento quando coberta de gelo.
Passo 2
Primeiro vamos usar a eq. (1) para obtermos o valor de . Se a origem é no ponto mais baixo, o ponto tem coordenada igual a 10 m e o ponto tem coordenada igual a 40 m. Além disso a distância entre os dois pontos é de 200 m:
Pela fórmula (1):
Primeiro aplicamos a fórmula para :
Agora para , mas trocando por :
Trocamos por , e então resolvemos numericamente as duas equações com auxílio de um computador. Então obtemos os valores:
Então descobrimos também o valor de :
Passo 3
Agora vamos olhar para a equação (2):
Como o cosseno hiperbólico é uma função que cresce com o aumento do módulo de , a tração máxima vai ocorrer o mais longe possível da origem, ou seja, no ponto . Então jogamos na fórmula o valor e , já substituindo pelo valor encontrado de :
Então obtemos através de :
Passo 4
Agora temos o valor total do peso por metro no cabo. Esse peso será do peso do próprio cabo mais o peso do gelo:
Então:
Como calculamos os valores de e sem precisarmos do valor de , a quantidade de gelo não mudará a configuração do fio, apenas mudando m módulo da tração em cada ponto.
Resposta
A quantidade de gelo não muda a configuração do fio.