Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 124
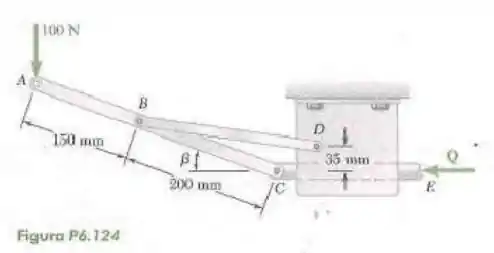
124- A barra de comando passa através do mancal horizontal no corpo do sistema de alternância mostrado na figura. Sabendo que a haste de ligação tem comprimento de , determine a força necessária para manter o sistema em equilíbrio quando .
Passo 1
Fazendo o diagrama de forças na barra temos:
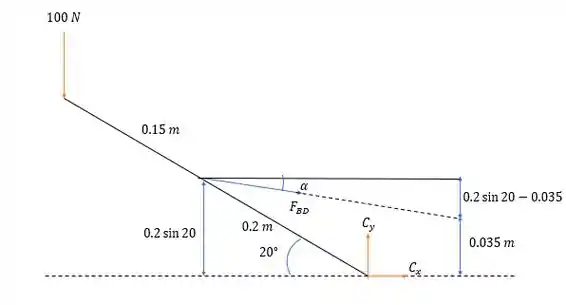
O ângulo que a força em faz com a horizontal vale:
Dessa forma a somatória dos momentos em será:
Então a força será:
Passo 2
Antes de analisar as forças no mancal nós precisaremos analisar pelo menos a força horizontal em , pois esse apoio está encostado na fonte de força que gera a força .
Pela somatória das forças horizontais temos:
Logo as forças na barra serão iguais a:
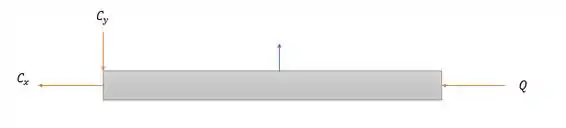
Pela somatória das forças horizontais temos:
Sentido para a esquerda mesmo.
Resposta
Exercícios de Livros Relacionados
Determine as distâncias x e y para que haja equilíbrio se F 1 = 800NeF 2 = 1000N .Fonte: Estática Mecânica para Engenharia – 14ª ed
Determine a intensidade F 1 e a distância y se x = 1,5 m e F 2 = 1000N . Fonte: Estática Mecânica para Engenharia – 14ª ed
Se o cabo CB está submetido a uma tração que é o dobro da do cabo CA, determine o ângulo para o equilíbrio do cilindro de 10 kg. Além disso, quais são as trações nos cabos CA e CB?
O mancal de rolamento consiste em esferas confi nadas simetricamente dentro da capa. O inferior está submetido a uma força de 125 N em seu contato A, em razão da carga sobre o eixo. Determine a