Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 123
123- Resolva o Problema quando .
Passo 1
Vamos fazer a mesma coisa que fizemos na questão anterior a diferença será bem sutil.
Pela somatória dos momentos em temos:
Dessa forma pela somatória das forças horizontais teremos:
Sacou a diferença?
E pela somatória das forças verticais:
Passo 2
Agora as forças na barra .
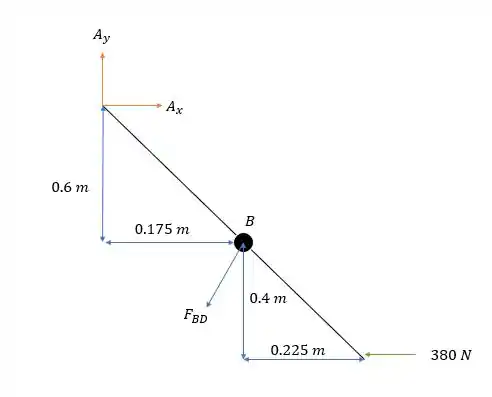
A somatória dos momentos em nos dá:
Isso nos dá:
Logo:
Passo 3
Cujo módulo em será igual a:
E essa será a força que estará presente na barra e o ângulo será o mesmo, a ação da barra será o inverso da presente no apoio em .
Dessa forma será:
Resposta
Exercícios de Livros Relacionados
Determine os componentes das reações em A e E quando uma força de 750N direcionada verticalmente para baixo é aplicada a em B , b em D .
A treliça mostrada na figura foi projetada para suportar um telhado de um supermercado. Para o carregamento dado, determine a força no elemento F G ,E GeE H .
Resolva o problema 6.168 considerando que a carga de 90 k N é substituída por um binário no sentido horário de intensidade 135 k N ⋅ m aplicado no elemento E D C no ponto D .
A treliça mostrada na figura foi projetada para suportar um telhado de um supermercado. Para o carregamento dado, determine a força no elemento K M ,L MeL N .
Uma prateleira de 20 k g é mantida na horizontal por uma mão francesa dobrável que consiste em duas partes E D C e C D B articuladas em C e apoiadas um contra a outra em D . Determine a força P necess