Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 3.Problemas - Ex. 36

Determine as distâncias x e y para que haja equilíbrio se F 1 = 800   N   e   F 2 = 1000   N .

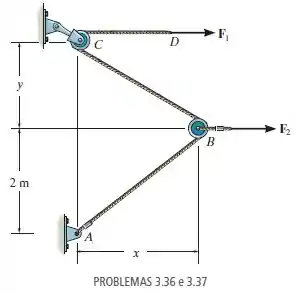
Fonte: Estática Mecânica para Engenharia – 14ª ed

Passo 1

Fala aí, Tudo de boas até agora?!

Espero que sim haha!

Bora lá!

Bem, a respeito de decomposição de forças, mais uma vez vamos lembrar, até abusar, sempre das 3 coisas para a melhor resolução de problemas envolvendo força resultante:

  1. Regra do paralelogramo;
  2. Lei dos senos;
  3. Lei dos cossenos.

O problema pede as distâncias x e y para que o sistema esteja em equilíbrio. E adivinha como vamos analisar essa questão??

Isso mesmo!! Pelo diagrama do corpo livre:

Passo 2

Agora vamos fazer o somatório de forças no eixo x e no eixo y:

∑ F y = 0   ;           F 1 c o s α = F 1 c o s β                       → α = β

Como os ângulos são iguais e possuem um cateto igual, então por simetria, temos que y = 2 m .

Então, o somatório de forças no eixo x:

∑ F x = 0   ;           2 * 800 * s e n β = 1000               → β = 38,68 0

Então, como β = 38,68 0 , podemos encontrar x :

t a n 38,68 = x 2             → x = 1,6   m

Resolvendo, então, encontramos:

x =   1,6   m     e     y = 2 m

Resposta

Portanto:

x =   1,6   m     e     y = 2 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O pino em B é fixado ao elemento A B C e pode deslizar livremente ao longo do rasgo aberto na placa fixa. Desconsiderando o efeito do atrito, determine o binário M necessário para manter o sistema em
O braço A B C está ligado por pinos ao colar em B e à manivela C D em C . Desprezando o efeito do atrito, determine o binário M necessário para manter o sistema em equilíbrio quando θ = 90 ° .
O pino em B é fixado ao elemento A B C e pode deslizar livremente ao longo do rasgo aberto na placa fixa. Desconsiderando o efeito do atrito, determine o binário M necessário para manter o sistema em
Duas hastes estão ligadas por um bloco deslizante como mostra a figura. Desprezando o efeito do atrito, determine o binário M a necessário para manter o sistema em equilíbrio.
O braço A B C está ligado por pinos ao colar em B e à manivela C D em C . Desprezando o efeito do atrito, determine o binário M necessário para manter o sistema em equilíbrio quando θ = 0 ° .