Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 125
125- Resolva o Problema quando ,
Passo 1
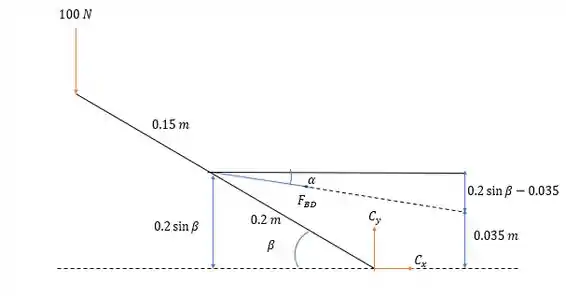
Aproveitando as contas e os desenhos feitos na questão anterior nós temos que:
Imaginando que o sinal positivo é o valor negativo trigonométrico. O sinal se mantém na conta.
E pela somatória dos momentos em temos que a força em será:
E logo pela soma das forças horizontais:
E que o valor de será igual a:
Esse é o algoritmo (por assim dizer) dessa questão.
Passo 2
Logo para nós iremos ter:
Dessa forma será:
E a reação :
Dessa forma a força será:
Com sentido para a esquerda.
Passo 3
Agora para .
Isso nos dará uma força igual:
A reação horizontal será:
Então a força será:
Com sentido para a esquerda.
Resposta
Exercícios de Livros Relacionados
Uma carga vertical P é aplicada na extremidade B de uma haste B C . A constante de mola é k , e a mola não fica deformada quando θ = 90 ° . ( a ) Desprezando o peso da haste, expresse o ângulo θ corre
25. Uma haste de um quarto de círculo de peso W e seção transversal uniforme é apoiada tal como mostra a figura. Determine o momento fletor no ponto J quando θ = 30 ° .
Determine as forças nos cabos AB e AC necessárias para suportar o semáforo de 12 kg.Fonte: Estática Mecânica para Engenharia – 14ª ed
A carga tem uma massa de 15 kg e é elevada pelo sistema de polias mostrado na figura. Determine a força F na corda em função do ângulo θ . Desenhe a função da intensidade F contra o ângulo θ para 0 ≤