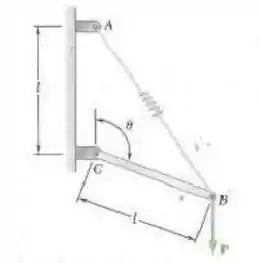
Uma carga vertical P é aplicada na extremidade B de uma haste B C . A constante de mola é k , e a mola não fica deformada quando θ = 90 ° . ( a ) Desprezando o peso da haste, expresse o ângulo θ correspondente ao equilíbrio em termos de P ,k el . ( b ) Determine o valor de θ correspondente ao equilíbrio quando P = 1 4 k l

θ = 2 sin - 1 ⁡ 1 2 k l k l - P θ = 141.1 °

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 56

Uma carga vertical é aplicada na extremidade de uma haste . A constante de mola é , e a mola não fica deformada quando . Desprezando o peso da haste, expresse o ângulo correspondente ao equilíbrio em termos de e. Determine o valor de correspondente ao equilíbrio quando

Passo 1

Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente deduza equação em função de e determine o valor de correspondendente ao equilíbrio. Para isso, devemos fazer o dcl:

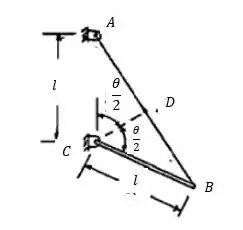
Sendo assim, temos:

E então:

Para a tensão:

Passo 2

Agora, para vamos usar as fórmulas de equilíbrio a fim de encontrar a equação:

Logo, temos:

E assim, . Ou então:

Passo 3

Para a segunda parte do problema, vamos usar a equação que a gente encontrou e substituir pelos valores que o nosso enunciado nos deu:

Resolvendo esta equação, temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

87- Uma haste delgada de comprimento L = 500m m é mantida em equilíbrio, tal como mostra a figura, com uma extremidade contra uma parede sem atrito e a outra presa a uma corda de comprimento S = 750m

85- Uma haste de massa 8k g e comprimento L é presa a cursores que podem deslizar livremente ao longo das guias mostradas nas figuras. Sabendo que a haste está em equilíbrio nas figuras. Sabendo que a

84- Uma haste delgada de comprimento L é presa a cursores que podem deslizar livremente ao longo das guias mostradas na figura. Sabendo que a haste está em equilíbrio, deduza uma expressão para o ângu

86- Uma haste delgada de comprimento L é mantida em equilíbrio, tal como mostra a figura, com uma extremidade contra uma parede sem atrito e a outra presa a uma corda de comprimento S . Deduza uma exp

90- Sabendo que para a haste do Problema 4.89 , L = 375m m , R = 500m m , e W = 45N , determine a ) o ângulo θ correspondente ao equilíbrio, b ) as reações em A e B .