Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 3.Problemas - Ex. 42
A carga tem uma massa de 15 kg e é elevada pelo sistema de polias mostrado na figura. Determine a força F na corda em função do ângulo . Desenhe a função da intensidade F contra o ângulo para .
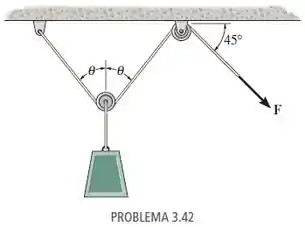
Fonte: Estática Mecânica para Engenharia – 14ª ed
Passo 1
E aí amores, bora pra mais uma?!
Bem, podemos analisar o problema e perceber que há tração na polia e que podemos começar analisando onde há a carga de massa 15kg.
O problema quer função da intensidade F contra o ângulo . Primeiramente façamos o diagrama do corpo livre:
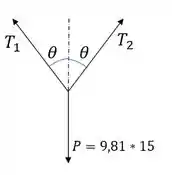
Fazendo o somatório de forças em cada eixo:
E
Passo 2
Agora analisando a força F em relação a tração da corda:
Vamos ao somatório de forças em relação a x:
Como já sabemos a relação entre T e , podemos utilizar a eq. 1 aqui, assim:
Resposta
Portanto:
Exercícios de Livros Relacionados
Determine a expressão para a intensidade do binário M que deve ser aplicado para equilíbrio.
Determine o valor do binário M que deve ser aplicado para que o membro DEFG esteja em equilíbrio.
Determine as reações em A e C quando (a) α = 0 , (b) α = 0 Figura P4.143
Um carrinho de mão é usado para transportar dois barris, cada qual de massa 40 kg. Desprezando a massa do carrinho, determine (a) a força vertical P que deve ser aplicada à barra para se manter o equi
Uma alavanca AB é articulada em C e presa a um cabo de controle em A. Se a alavanca for submetida a uma força vertical de 300 N em B, determine (a) a tração no cabo, (b) a reação em C