Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 137
137. Determine o ângulo entre os segmentos de tubo e .
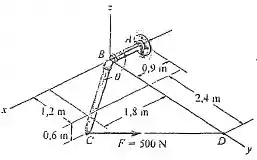
Passo 1
Para achar esse ângulo precisamos lembrar de como calcular o produto escalar entre dois vetores. Assim:
Onde é o ângulo entre os dois vetores, isolando temos:
Então para realizar essa conta precisamos achar o vetor que sai do ponto até o ponto e o vetor que sai do ponto até o ponto .
Passo 2
é o vetor que sai do ponto até o ponto . Assim:
é o vetor que sai do ponto até o ponto . Assim:
Passo 3
Agora basta usar a fórmula do passo 1 para achar .
Resposta
Exercícios de Livros Relacionados
Se F = {350i - 250j - 450k} N e o cabo AB tem 9 m de extensão, determine as coordenadas x, y, z do ponto A.
Determine a intensidade e os ângulos diretores coordenados da força resultante que atua sobre o olhal.
Expresse cada força na forma de vetor cartesiano.
Expresse cada força na forma de vetor cartesiano.
Determine a intensidade e os ângulos diretores coordenados da força resultante, e desenhe esse vetor no sistema de coordenadas.