Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 140
140. Determine a intensidade da força F como uma função do tempo, que dever ser aplicada à extremidade da corda em A para levantar o gancho H com uma velocidade constante . Inicialmente, a corrente está em repouso sobre o solo. Despreze a massa da corda e do gancho. A corrente tem massa de 2kg/m.
Passo 1
Neste tipo de problema seria importante fazer um esboço da situação que o enunciado descreve para sabermos quais são as forças que estão envolvidas no problema e a partir daí utilizar as equações desenvolvidas ao longo da seção.
Passo 2
Um esboço do que está sendo dito no enunciado pode ser representado por:
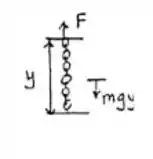
Passo 3
Do enunciado, podemos tirar que:
Passo 4
Da equação 15.28, temos que:
Da equação 15.28, temos que:
Resposta
Exercícios de Livros Relacionados
Um caminhão-baú está viajando a 96 km/h quando o motorista aciona os freios. Sabendo que as forças de frenagem do caminhão e do baú são de 18 kN e 68 kN, respectivamente, determine (a) a distância per
Os dois blocos mostrados na figura estão originalmente em repouso. Desprezando as massas das roldanas e o efeito do atrito nessas roldanas e entre o bloco A e a superfície horizontal, determine (a) a
Os coeficientes de atrito entre a carga e o reboque de piso plano mostrado na figura são μ s = 0,40 e μ k = 0,30. Sabendo que velocidade escalar do equipamento é 72 km/h, determine (a) a menor distânc
A aceleração de um pacote deslizando no ponto A é 3 m/s2. Considerando que o coeficiente de atrito cinético é o mesmo em cada seção, determine a aceleração do pacote no ponto B.
Se a distância de frenagem de um automóvel a 96 km/h é de 45 m em um piso nivelado, determine a distância de frenagem desse automóvel a 96 km/h quando ele está (a) subindo um plano inclinado de 5° e (