Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 10
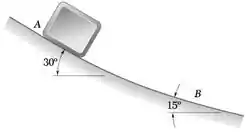
A aceleração de um pacote deslizando no ponto A é 3 m/s2. Considerando que o coeficiente de atrito cinético é o mesmo em cada seção, determine a aceleração do pacote no ponto B.
Passo 1
Para qualquer ângulo .
Use as coordenadas x e y conforme mostrado.
Passo 2
No ponto A.
Passo 3
No ponto B.
Resposta
Exercícios de Livros Relacionados
Uma bola de 125g que se move a uma velocidade de 3m / s atinge uma placa de 250g sustentada por molas. Admitindo que não haja perda de energia no impacto, determine ( a ) a velocidade da bola imediata
Um jogador de beisebol, ao pegar uma bola, pode amortecer o impacto levando sua mão para trás. Considerando que uma bola de 140g atinge sua luva a 140k m / h e que o jogador puxa sua mão para trás dur
A fim de testar a resistência ao impacto de uma corrente, ela é suspensa por uma viga rígida de 120k g apoiada em duas colunas. Uma barra presa no último elo é, então, golpeada por um bloco de 30k g q
Uma bala de massa m é atirada com velocidade v 0 formando um ângulo com a horizontal e se aloja em um bloco de madeira de massa M . O bloco pode rolar sem atrito no piso duro e é impedido por molas de
Uma bolinha de 50 g atirada verticalmente por uma pistola de mola na superfície da Terra atinge a altura de 100 m. A mesma bolinha atirada pela mesma pistola na superfície da Lua atinge a altura de 68