Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 140
140. Determine a intensidade mínima e a direção da força de modo que a resultante de todas as três forças tenha uma intensidade de .
Passo 1
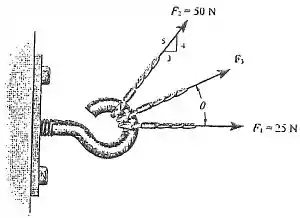
Fala ai galerinha bonita, tudo beleza?! Saca só, nesse exercício aqui o enunciado nos deu forças atuando sobre um suporte, como na figura abaixo:
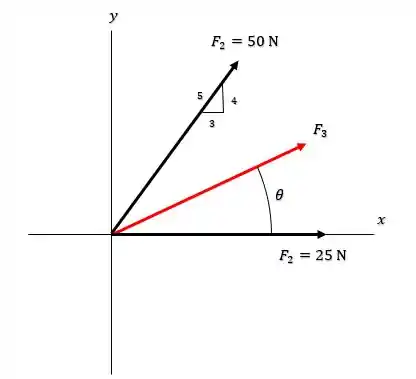
Sabemos o módulo e a direção da força e da força , e a partir disso o enunciado nos pede pra descobrir a menor intensidade e a direção da força possível que faz com que o módulo da força resultante entre essas forças seja igual a , ou seja:
Então bora lá ver como que fica essa brincadeira ai!
Passo 2
Bom galerinha, como conhecemos as duas forças e podemos encontrar a resultante entre elas, tal que:
Onde e são dadas como:
Dando mais uma arrumadinha, teremos que:
Logo será:
E o módulo dessa força é dada por:
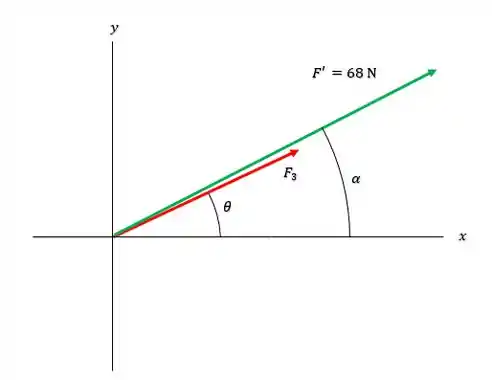
Então isso quer dizer que podemos substituir as forças e pela força no nosso diagrama:
Passo 3
Mas agora que vem a malandragem do exercício.
Porque a maneira mais curta de fazer o vetor resultante entre e atingir o módulo de , é se as duas forças estiverem no mesmo sentido, ou seja, para a intensidade de ser mínima, precisamos que :
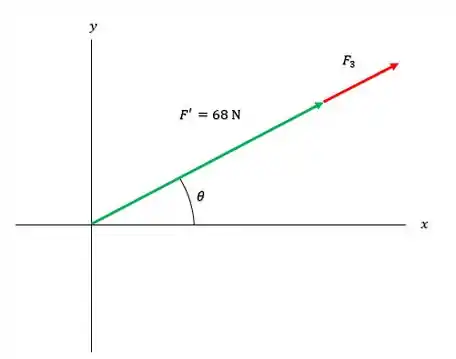
Ou seja, para que isso seja igual a , teremos que:
Logo:
Portanto, a intensidade mínima para é de .
Passo 4
E o ângulo de orientação, como deve ser o mesmo da força , podemos obter através da relação:
De modo que
Resposta
A intensidade mínima da força é:
E sua direção em relação ao eixo é: