Um grupo de estudantes carrega um reboque de com duas caixas de e uma caixa de . Cada caixa est[a colocada na traseira do reboque e alinhada pelos seus limites traseiro e lateral. Determine a menor carga que os estudantes devem colocar em uma segunda caixa de e em que lugar do reboque eles devem posicioná-la sem que nenhuma parte da caixa se projete para fora dos limites do reboque, considerando-se que cada caixa é carregada uniformente e que a linha de ação da resultante dos pesos das quatro caixas deve passar pelo ponto de interseção da linha de centro do reboque com o eixo de rodas. (Dica: a caixa pode ser colocada nas laterais ou no fim do reboque.)
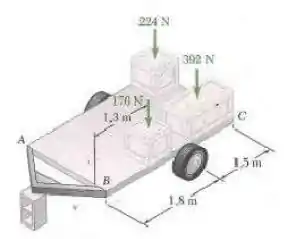
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Sabemos que a resultante é a soma das três forças que representam os pesos das crianças, portanto:
Para determinarmos a distância , igualaremos o momento em torno do eixo para ambos os sistemas equivalentes apresentados no item anterior:
Resolvendo, temos que:
Passo 2
Para determinarmos a distância , igualaremos o momento em torno do eixo para ambos os sistemas equivalentes apresentados no item anterior:
Resolvendo, temos que:
Passo 3
Do enunciado do problema, nós sabemos que a resultante de total composta por e passa através do ponto . E como a resultante total passa por , temos que .
Além do mais, como a carga tem que ser a menor possível, a quarta caixa deve ser colocada o mais longe possível do ponto . Isso indica que a caixa deve estar na região:
Passo 4
Vamos testar primeiramente .
Sabemos que , portanto, vamos fazer um somatóriio de momentos no ponto ao redor do eixo :
Precisamos agora, checar a possibilidade física desse valor, para isso, façamos um somatório de momentos no ponto , desta vez ao redor do eixo :
O que não é possível, pois a condição não é atendida.
Passo 5
Vamos testar então .
Sabemos que , portanto, vamos fazer um somatóriio de momentos no ponto ao redor do eixo :
Precisamos agora, checar a possibilidade física desse valor, para isso, façamos um somatório de momentos no ponto , desta vez ao redor do eixo :
Como este resultado respeita a condição , então a solução é possível.
O peso mínimo da quarta caixa é de e a posição da caixa deve ser de tal forma que o lado menor esteja no sentido de e o centro da caixa esteja afastado de .