Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 149
149. A pressão do vento atuado sobre um painel triangular é uniforme. Substitua esse carregamento por uma força e momento de binário resultante equivalentes no ponto .
Passo 1
Para podermos substituir esse carregamento por uma força resultante, basta calcular a intensidade da força desse carregamento, aí teremos a força resultante que o enunciado pede.
Para calcular o momento de binário pedido, temos que achar o ponto de atuação dessa força resultante, para sabermos a que distancia do ponto essa força se encontra e aí sim calcular o momento por meio da análise vetorial.
A intensidade da força vai ser igual, nesse caso, ao volume total sob o diagrama de carregamento, nesse caso vai ser o volume em vez da área devido a geometria do nosso diagrama.
A posição do centroide em relação ao próprio diagrama, que é onde essa força atua é dada pela seguinte fórmula:
Mas para figuras geométricas mais simples, como o nosso caso, tem fórmulas tabeladas que você pode encontrar no apêndice C na seção C.4.
Como o painel é triangular, a posição do centroide é dada por:
Passo 2
Pelo o que foi dito no passo 1, vamos achar a intensidade da força através do volume da figura formada, então:
Onde é base do triângulo, é a altura do triângulo e é a altura do volume (isso pode ser constatado na imagem que o livro fornece).
Vamos passar essa intensidade que encontramos para forma vetorial, como você pode ver na figura, se juntarmos todas aquelas setinhas pequenas vamos ter uma seta grande e que aponta somente na direção negativa de , logo:
Passo 3
Agora vamos calcular em que posição essa força atua no painel em relação ao próprio painel e depois vemos em que posição ela atua em relação ao ponto .
Usando a fórmula mencionada no passo 1, podemos achar essa posição de atuação da força. Se você reparar o painel é um triângulo isósceles, então tanto faz qual desses dois lados iguais escolher para achar a posição do centroide, isso é até bom porque podemos achar sua posição em relação ao eixo e ao eixo .
Calculando essa posição:
Afigura abaixo mostra essa distância de melhor forma, levando em conta o que foi dito acima.
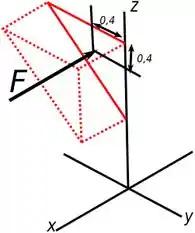
Agora temos que achar essa posição em relação ao ponto , mas isso se torna fácil quando temos as distancias fornecidas pela imagem do enunciado, usando aquilo ao nosso favor, temos que:
Passo 4
Agora vamos calcular o momento de binário com análise vetorial, então: