Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas Revisão - Ex. 149
149. Resolver o problema , considerando que a força de é dirigida para cima
Passo 1
E aí meus queridos! Aqui vamos nós de novo, resolver nossa antepenúltima questão desse finalzinho de capítulo.
E a missão aqui é resolver a mesma questão anterior, com apenas um dado alterado.
Temos que achar as tensões normal e de cisalhamento nos pontos e , se a força de , que antes estava apara baixo, apontar para cima.
Podemos fazer isso, simplesmente usando as fórmula abaixo...
Eu disse simples, né!! Pois é! falei uma grande besteira.
Simples, vai ser substituir os valores numéricos de cada variável! Encontrar o quanto vale cada uma, vai dar um trabalhão!
Bom! Vamos ver por onde começar!
Nas duas fórmulas, temos alguns termos que dependem diretamente da seção transversal, como o momento polar , a área da seção transversal , os comprimentos e o momento de inércia .
Logo, é por aí que vamos dar nosso primeiro passo!
Passo 2
Bora começar, fazendo o esboço da seção transversal...
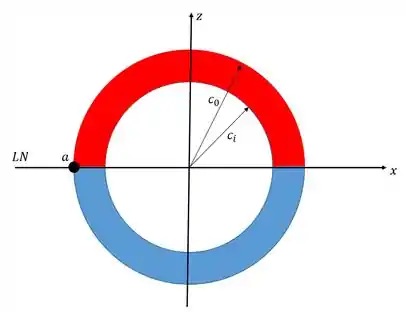
A região destacada em vermelho, é a região acima da linha neutra, que pega metade da figura, coisa que a gente já está acostumado a fazer.
Mas nesse caso, estamos analisando apenas o ponto . E nesse caso a linha neutra vai ficar sobre o eixo .
Se pegássemos o ponto , a linha neutra ficaria sobre o eixo e a região esboçada em vermelho não seria a mesma, mas teria a mesma área.
Aí você deve tá se perguntado. Porque não fazer outro desenho!?
Ora bolas! Isso é um círculo! As propriedades que nos estamos trablhando aqui; como área, momento de inércia e momento polar não mudam.
Entendeu agora?
Pois muito bem! A questão nos diz que o tubo tem diâmetros, interno e externo, iguais a e .
Desse modo, o raio externo vai valer...
Já o raio interno ...
E assim, podemos obter o valor de , e através das seguintes fórmulas abaixo...
Onde substituindos os valores de e ...
Obtemos os seguintes valores para nossas variáveis
Outra coisa que podemos calcular é o momento estático e a espessura... Essas duas propriedades também não variam, independentemente se pegarmos os pontos ou ...
No caso, como temos uma coroa de um semicírculo, para calcular o temos que usar a fórmula abaixo...
Substituindo os valores já conhecidos...
No caso do , basta subtrair o diâmetro externo do interno e iremos obter a espessura da seção nos pontos e ...
Passo 3
A próxima coisa a se fazer agora, é tentar encontrar as seguintes variáveis que estão faltando...
A força mais de boas de obter é a força ! Ela é a força vertical agindo em nosso sistema, no caso a de .
E como ela está apontando para cima e o eixo tem referencial positivo para cima, então...
A primeira já foi!
Continuando nosso raciocínio, bora ver qual é mais em conta de se obter, das quatro que sobraram!
Sei não, hein!? Eu diria que é a força cortante, já que aquela força de está sendo aplicada paralelamente à superfície da manivela, com direção no eixo .
É isso mesmo!
Desse modo, fazendo o somatório das forças para o eixo , obtemos que...
Como não tem nenhuma força em , então...
Agora, vamos pras tensões! O que queremos aqui é transferir as tensões e momentos gerados devido as forças pros nossos pontos e .
Bem! A primeiro tensão que podemos encontrar é a torção , quando um momento é gerado em torno do eixo .
A força responsável por esse momento é a de , e ela está a uma distância de , com tendência de giro no sentido anti-horário. Sendo assim...
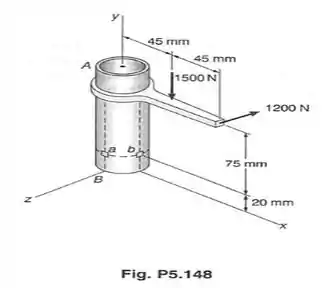
Depois, bora encontrar o momento em relação ao eixo , . Olhando a figura do enunciado, podemos ver que a força que contribui para gerar momento nesse eixo, é a força de , que está a uma distância de dos nossos pontos e , com tendência de giro no sentido horário...
No eixo , a força responsável por gerar momento é a de . E essa força está a uma distância de do eixo com tendência de giro no sentido anti-horário. Logo...
Pronto! Conseguimos obter todas as variáveis!
Passo 4
a) Vamos então, substitui-lás para obter as tensões no ponto ...
Um adendo aí! e na primeira fórmula são as coordenadas do ponto no nosso sistema. Olhando a figura do enunciado, podemos ver que elas valem...
Logo, trocando cada variável por seu correspondente valor...
Obtemos que...
Passo 5
b) Fazendo a mesma coisa para o ponto , cujas coordenadas são...
E usando as fórmulas abaixo...
Substituindo os valores numéricos...
Chegamos até às resposta abaixo...
Resposta
a)
b)