Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 55a

Uma barra de aço ( E a = 200   G P a ) e uma de alumínio ( E a l = 70   G P a ) são firmemente unidas para formar a viga composta mostrada. Para uma força cortante vertical de 20   k N , determinar (a) a tensão média na superfície de contatos; (b) a máxima tensão de cisalhamento na viga. (Sugestão: Usar o método indicado Prob. 5.52)

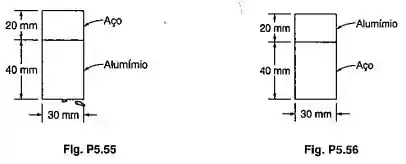
Passo 1

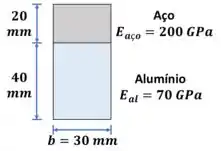
Pra começar, vamos transformar a região de alumínio em aço. Pra isso, precisamos calcular o fator entre os módulos de elasticidade:

n = E a l E a ç o = 70 200 = 0 , 35

E calculamos a nova base da região de alumínio:

b 2 = n ⋅ b = 0 , 35 ⋅ 30 = 10.5   m m

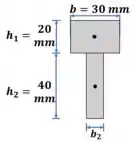
Passo 2

Beleza! Agora é só prosseguir como uma questão normal!

Vamos calcular o centroide:

y - = h 1 b ⋅ y - 1 + h 2 b 2 ⋅ y - 2 h 1 b + h 2 b 2

y - = 40 ⋅ 10,5 ⋅ 20 + 20 ⋅ 30 ⋅ 50 40 ⋅ 10.5 + 20 ⋅ 30

y - = 37,65   m m

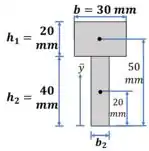
E com isso podemos calcular o momento de inércia:

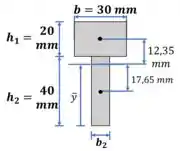
I = 30 ⋅ 20 3 12 + 30 ⋅ 20 ⋅ 12,35 + 10,5 ⋅ 40 3 12 + 10.5 ⋅ 40 ⋅ 17,65

I = 298352,95   m m 4

Passo 3

Agora temos que calcular o momento estático na região de contato.

Vamos destacar em laranja a região de interesse.

Q = 30 ⋅ 20 ⋅ 12,35

Q = 7410     m m 3

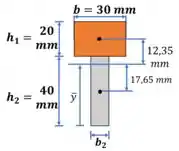
Passo 4

Ok! Todas as propriedades geométricas já foram calculadas, então precisamos parar de utilizar a figura modificada.

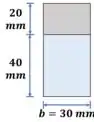
E pra finalizar a questão, é só calcular a tensão. Como não usamos a seção transformada, então t = 30   m m deve ser usado

τ = V Q I t

τ = 20   k N ⋅ 7410   m m 3 298352,95   m m 4 ⋅ 30   m m

τ = 16,5 6   M P a

Resposta

τ = 16,56   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As fibras de uma peça de madeira formam um ângulo de 18 graus com a vertical. Para o estado de tensões mostrado determinar: (a) a tensão de cisalhamento no plano, em um plano paralelo as fibras;(b) a
Duas peças de madeira de 80x120mm, de seção transversal retangular e uniforme, são unidas por simples colagem das seções chanfradas, como mostrado. Sabendo-se que as máximas tensões admissíveis na jun
Um tubo de aço de 300mm de diâmetro externo é fabricado com chapa fina de 6,35mm de espessura, soldada ao longo de uma hélice que forma um ângulo de 22,5 graus com um plano perpendicular ao eixo do tu
As seções transversais de duas vigas extrudadas, cada uma com espessura da parede uniforme e igual a 6,35 m m são mostradas. Para uma força cortante vertical de 11120N , determinar a máxima tensão de
Para a viga de seção transversal mostrada, submetida a uma força cortante vertical de 25k N , determinar a tensão de cisalhamento, quando d = 50 m m , no:Ponto b