Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 147

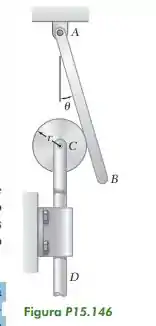
15.147. No Problema 15.146, deduza uma expressão para a aceleração angular da barra AB.

Passo 1

Vamos lá! Da para ver pela imagem que

r = y sin ⁡ θ

Então

y = r sin ⁡ θ

E aí podemos fazer

y ˙ = d d t r sin ⁡ θ

Essa derivada fica o seguinte

y ˙ = r d d t 1 sin ⁡ θ

Usando a regra da cadeia

y ˙ = r d d θ 1 sin ⁡ θ ⋅ d d t θ

Então

y ˙ = - r cos ⁡ θ sin 2 ⁡ θ ⋅ d θ d t

Passo 2

A gente pode assumir que

d θ d t = ω

E

y ˙ = - v 0

Então temos

v 0 = r cos ⁡ θ sin 2 ⁡ θ ⋅ ω

Isolando ω

ω = v 0 sin 2 ⁡ θ r cos ⁡ θ

Passo 3

Mas a aceleração angular pode ser obtida da seguinte maneira

α = d ω d t

E podemos fazer o seguinte

d ω d t = d ω d θ ⋅ d θ d t

E aí temos

d ω d t = d ω d θ ⋅ ω

Então

α = d d θ v 0 sin 2 ⁡ θ r cos ⁡ θ ⋅ v 0 sin 2 ⁡ θ r cos ⁡ θ

Essa derivada fica

α = v 0 r 2 cos 2 ⁡ θ sin ⁡ θ + sin 3 ⁡ θ cos 2 ⁡ θ v 0 sin 2 ⁡ θ r cos ⁡ θ

Isso fica

α = v 0 r 2 2 cos 2 ⁡ θ   sin 3 ⁡ θ + sin 5 ⁡ θ cos 3 ⁡ θ

Vamos colocar sin 3 ⁡ θ em evidencia

α = v 0 r 2 sin 3 ⁡ θ 2 cos 2 ⁡ θ + sin 2 ⁡ θ cos 3 ⁡ θ

A gente pode dizer que

sin 2 ⁡ θ = 1 - cos 2 ⁡ θ

Então

α = v 0 r 2 sin 3 ⁡ θ 2 cos 2 ⁡ θ + 1 - cos 2 ⁡ θ cos 3 ⁡ θ

Isso fica α = v 0 r 2 sin 3 ⁡ θ 1 + cos 2 ⁡ θ cos 3 ⁡ θ

Ou

α = v 0 r 2 1 + cos 2 ⁡ θ   tan 3 ⁡ θ

Resposta

α = v 0 r 2 1 + cos 2 ⁡ θ   tan 3 ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.161. No instante mostrado na figura, o comprimento da lança AB está sendo aumentado a uma taxa constante de 0,2 m/s e a lança está sendo baixada a uma taxa constante de 0,08 rad /s. Determine (a) a
A placa retangular mostrada na figura gira à taxa constante ω 2 = 12r a d / s em relação ao braço A E , que, por sua vez, gira à taxa constante ω 1 = 9r a d / s em torno do eixo Z . Para a posição mos
Resolva o Problema 15.222, considerando que, no instante mostrado, a velocidade angular ω 1 da placa de 10r a d / s está decrescendo a uma taxa de 25r a d / s 2 , enquanto a velocidade relativa u do p
Usando o método da Seção 15.14 , resolva o Problema 15.19 2 .
Uma placa quadrada com 500m m de lado está articulada nos pontos A e B de um grampo em U . A placa gira à taxa constante ω 2 = 4r a d / s em relação ao grampo, que, por sua vez, gira à taxa constante