Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 47

15.47. No Problema 15.46, determine (a) a velocidade do ponto B, (b) o ponto da placa com velocidade nula.

Passo 1

Vamos matar mais uma?

Antes de começar a resolver vamos relembrar os resultados que a gente conseguiu no problema 15.46.

ω → = - 2   k ^ r a d s

v A = 120   i ^ + 660   j ^ m m s

O item (a) pede para a gente calcular a velocidade em B. Para isso podemos usar essa equação

v B → = v A → + v B A →

Mas

v B A → = ω → × r B A →

Então

v B → = v A → + ω → × r B A →

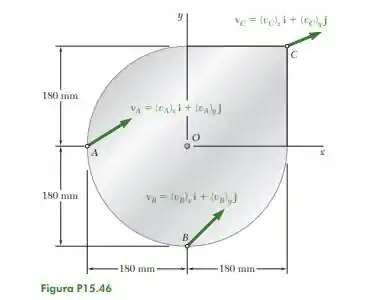
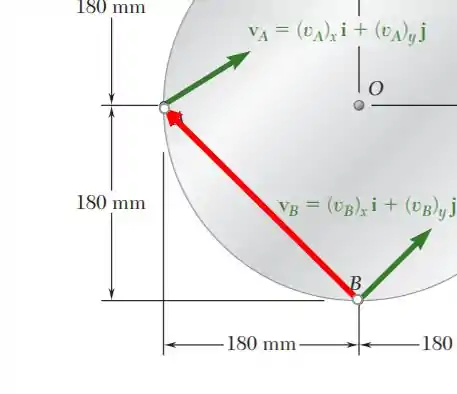
Olhando a imagem, a gente pode determinar

r B A → = 180   i ^ - 180   j ^   m m

Passo 2

Agora vamos substituir os valores na nossa equação

v B → = v A → + ω → × r B A →

v B → = 120   i ^ + 660   j ^ + ( - 2   k ^ ) × 180   i ^ - 180   j ^

Isso fica

v B → = 120   i ^ + 660   j ^ + - 360   i ^ - 360   j ^

Então

v B → = - 240   i ^ + 300   j ^ m m s  

Passo 3

Agora vamos para o item (b), determinar em que ponto da placa a velocidade é nula. Vamos chamar esse ponto de P → , em que

P → = x   i ^ + y   j ^

A velocidade nesse ponto é nula, então

v P → = 0

Mas, podemos calcular também

v P → = v A → + v P A →

Ou

v P → = v A → + ω → × r P A →

E a gente pode calcular

r P A → = r P → - r A →

Então

v P → = v A → + ω → × r P → - r A →

Mas como v P → = 0

v A → + ω → × r P → - r A → = 0

Passo 4

Vamos substituir os valores agora

120   i ^ + 660   j ^ + - 2   k ^ × x   i ^ + y   j ^ - ( 180   i ^ = 0

Então

120   i ^ + 660   j ^ + - 2   k ^ × 180 + x   i ^ + y   j ^ = 0

120   i ^ + 660   j ^ + 2   y   i ^ + - 360 - 2 x   j ^ = 0

Vamos resolver para cada componente, primeiro para a componente i ^ :

120 + 2 y = 0

Então

y = - 60   m m

Agora para j ^ :

660 - 360 - 2 x = 0

Então

x = 150   m m

Logo

P → = 150   i ^ - 60   j ^ m m

Resposta

a : v B → = - 240   i ^ + 300   j ^ m m s  

b : P → = 150   i ^ - 60   j ^ m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/71) A barra C B desliza através do cursor articulado fixado à barra O A . Se C B possui uma velocidade angular no sentido horário de 2r a d / s , determine a velocidade angular ω O A da barra O A qu
5/76) No instante representado , a placa triangular A B D possui uma velocidade angular no sentido horário de 3r a d / s . Determine para esse instante a velocidade angular ω B C da barra B C .
5/105) Determine a velocidade do ponto D no Prob.5/62 pelo método da seção 5/5 .
5/104) A extremidade A da vara delgada recebe uma velocidade v A para a direita ao longo dasuperfície horizontal . Mostre que o módulo da velocidade da extremidade B é igual á v A quando o ponto centr
5/102) O eixo do conjunto da roda sem deslizar sobre a superfície horizontal fixa . e o ponto O possui uma velocidade de 0,8m / s para a direita . Pelo método dessa seção , determine as velocidades do