Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 117
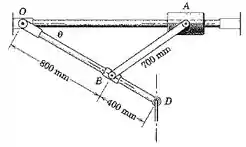
5/117) O projeto do mecanismo mostrado , o cursor deve deslizar ao longo do eixo fixo conform o ângulo aumenta . Quando , o elemento de controle em deve ter uma componente de velocidade para baixo de . Determine a velocidade correspondente do cursor pelo método dessa seção .
Passo 1
Então galera , primeiro vamos dar uma olhada na figura que ilustra a situação do problema :
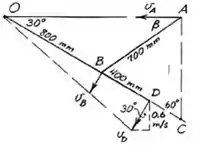
Como é possível observar acima, temos que :
Logo
Sendo assim , temos que :
Portanto ,
Passo 2
Bom pessoal , como a velocidade angular da barra é a mesma para todos os pontos temos que :
Logo ,
Seja o centro nstantâneo para , analisando a geometria da figura indicada no enunciado , obtemos que :
Como a velocidade angular é constante para o sistema , sabemos que :
Portanto ,
Resposta
Exercícios de Livros Relacionados
5/66) O módulo da velocidade absoluta do ponto A sobre o pneu de automóvel é de 12m / s quando A está na posição indicada . Quais são as correspondentes velocidade v O do caro e velocidade angular ω d
5/61) O vértice A da placa em formato de triângulo eqüilátero possui uma velocidade v A = 0,8m / s para a direita , e a velocidade angular no sentido anti-horário da placa é ω = 5r a d / s . Determine
5/69) O ciclista mostrado pedala regularmente para manter uma velocidade constante de 16k m / h em oposição a uma leve brisa frontal . Calcule os módulos máximo e mínimo da velocidade absoluta do peda
5/60) O carrinho possui uma velocidade de 1,2m / s para a direita . Determine a velocidade angular N da roda de modo que o ponto A no topo da borda tenha uma velocidade (a) igual a 1,2m / s para aesqu
5/64) A velocidade do centro da Terra enquanto orbita o sol é v = 107257k m / h e a velocidade angular absoluta da Terra em torno de seu eixo de rotação norte-sul é ω = 7,292 10 - 5 r a d / s . Utiliz