Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 111

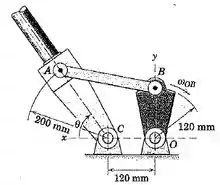
5/111) Os elementos do mecanismo para a implantação da lança do magnetômetro de uma nave espacial são reapresentados aqui a partir do Prob.5/87 . Pelo método dessa seção , determine a velocidade angular da lança quando o elemento de acionamento O B cruza o eixo y com uma velocidade angular ω O B = 0,5   r a d / s se nesse instante tan ⁡ θ = 4 / 3 .

Passo 1

Então galera , como aprendemos neste capítulo , sabemos que :

v = ω r

Sendo assim , temos que :

v B = B C 1 - ω = 0,120 0,5 = 0,060   m / s

Da mesma forma , sabemos que a velocidade angular do sistema é constante , logo :

ω C A = ω C B

Passo 2

Bom pessoal , analisando a equação obtida no passo anterior , achamos que :

v A A C 1 - = v B B C 1 -

Portanto ,

v A = A C 1 - B C 1 - v B = 0,400 0,280 0,060 = 0,0857   m / s

Agora substituímos os valores encontrados para acharmos a velocidade angular do sistema através da relação:

ω C A = v A A C 1 - = 0,0857 0,200 = 0,429   r a d / s

Resposta

ω C A = 0,429   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/62) O centro C da roda menor possui uma velocidade v c = 0,4 m/s na direção mostrada . O cabo que liga as duas rodas está firmemente enrolado em torno das respectivas periferias e não desliza . Calc
Um bloco B de 1,5 kg é conectado por um cabo a um bloco A de 2 kg, que está suspenso por uma mola de 3 kN / m constantes. Sabendo que o sistema está em repouso quando a corda é cortada, determine (a)
Conforme a velocidade de rotação de um motor apoiado por mola é lentamente aumentada de 200 para 500 rpm, a amplitude da vibração devido ao desequilíbrio do rotor é observada diminuindo constantemente
A roda de 80 mm de raio mostrada na figura rola para a esquerda com uma velocidade de 900 mm/s. Sabendo que a distância AD é 50 mm, determine a velocidade do cursor e a velocidade angular da barra AB
74. No instante mostrado, o caminhão se desloca para a direita a 3m/s, enquanto o cano rola no sentido anti-horário a ω = 8r a d / s sem deslizar em B. Determine a velocidade do centro G do cano.