Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 116
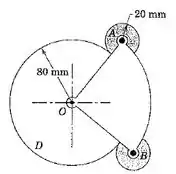
5/116) A engrenagem (os dentes não são mostrados) gira no sentido horário em torno de com uma velocidade angular constante de . O setor de está montado sobre um eixo independente em , e cada uma das pequenas engrenagens em e se acopla com a engrenagem . Se o setor possui uma velocidade angular no sentido anti-horário de no instante representado , determine a velocidade angular correspondente de cada uma das engrenagens pequenas.
Passo 1
Então galera , como aprendido neste capítulo , sabemos que :
Dessa forma , temos que :
Além disso nós sabemos que a velocidade angular do sistema é constante . Logo :
Passo 2
Bom pessoal , somando as equações (1) e (2) , obtemos que :
Sendo assim ,
Logo ,
Resposta
Exercícios de Livros Relacionados
5/68) A placa quadrada uniforme se desloca no plano x y e possui uma velocidade angular no sentido horário . No instante representado , o ponto A tem uma velocidade de 2 m / s para a direita , e a vel
5/65) As duas polias são rebitadas em conjunto para formar uma única unidade rígida , e cada um dos dois cabos está firmemente enrolado em torno de suas respectivas polias . Se o ponto A no cabo de el
5/67) A roda de raio r rola sem deslizar e possui uma velocidade angular ω . Escreva uma expressão para a velocidade do ponto A em termos de θ e mostre que as velocidades de A e B são perpendiculares
5/59) A extremidade A da haste possui a velocidade indicada no instante representado . A extremidade B está confinada a se deslocar na ranhura. Para esse instante calcule a velocidade de B e a velocid
5/63) Por um curto intervalo , os cursores A e B estão deslizando ao longo do eixo fixo vertical com velocidade v A = 2 m / s e v B = 3 m / s nos sentidos indicados . Determine o módulo da velocidade