Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 119

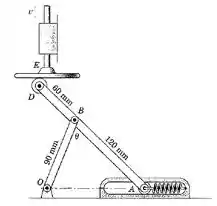
5/119) O movimento do rolete contra sua mola restritiva é controlado pelo movimento descendente do êmbolo . Para um intervalo de movimento a velocidade de é . Determine a velocidade de quando se torna .

Passo 1

Então galera , seja o centro instantâneo de velocidade nula para . Primeiramente , bora dar uma olhada na figura do problema :

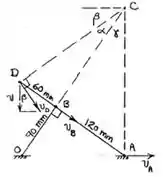
Pela geometria da figura e os valores já fornecidos, obtemos que :

Aplicando pitágora , achamos que :

Passo 2

Bom pessoal , agora usaremos as relações trigonométricas para achar os ângulos indicados na figura . Sendo assim , temos que :

Pela figura , identificamos que , logo :

Sendo assim , podemos achar a velocidade do ponto através da relação :

Como as velocidades angulares do sistema são as mesmas , temos que :

Logo ,

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/77) A manivela O A oscila em torno da posição θ = 0 obrigando C B , por sua vez , a oscilar . Se O A possui uma velocidade angular no sentido anti-horário de 6r a d / s quando θ = 30 ° , determine a

5/70) O disco circular rola sem deslizar com uma velocidade angular no sentido horário ω = 4r a d / s . Para o instante representado , escreva as expressões vetoriais para a velocidade de A com relaçã

5/75) Cada uma das barras deslizantes A e B se acopla na sua borda respectiva das duas rodas rebitadas sem deslizar . Determine o módulo da velocidade do ponto P para a posição indicada.

5/72) No instante representado , a velocidade do ponto A da barra de 1,2m é de 3m / s para a direita . Determine a velocidade v B do ponto B e a velocidade angular ω da barra . O diâmetro das pequenas

5/73) A unidade em A consiste em um motor com redução de alto torque que gira a barra A B na taxa constante θ ' = 0,5r a d / s . A unidade A é livre para se mover ao longo da superfície horizontal . D