Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 114
5/114) O cilindro pequeno rola sobre asuperfície do cilindro grande sem deslizar . Utilizando o centro instantâneo de velocidade nula do cilindro pequeno , determine a velocidade do ponto indicado quando e está crescendo na taxa .
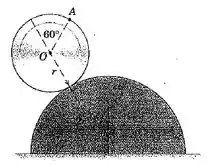
Passo 1
Então galera , como aprendemos neste capítulo , sabemos que :
Sendo assim , a velocidade do ponto é dada por :
Além disso , nós sabemos que a velocidade angular do sistema é constante , logo :
Passo 2
Bom pessoal , seja é o centro instantâneo de velocidade nula . Como visto anteriormente , sabemos que :
Sendo assim ,
Logo ,
Resposta
Exercícios de Livros Relacionados
Um braço uniforme ABC de 750 g é sustentado por um pino em B e está ligada a uma mola em A. O braço está unido em C a uma massa m de 1,5 kg que está ligado a uma mola. Sabendo que cada mola pode atuar
Um pêndulo invertido constituído de uma esfera de peso W e umabarra rígida ABC de comprimento l e peso desprezível é suportadopor um pino e suporte em C. A mola de constante k está ligada auma barra e
Para o pêndulo invertido do Problema 19.91 e para os valores dados de k, a e l, observa-se que f = 1,5 Hz quando m = 1 kg e que f = 0,8 Hz quando m = 2 kg. Determine o maior valor de m para o qual as
Uma barra uniforme ABC de 2 kg é sustentada por um pino em B e está ligada a uma mola em C. A barra está unida em A a um bloco DE de 2 kg que está ligado a uma mola e pode rodar sem atrito. Sabendo qu
Um eletroímã de 150 kg está em repouso e está segurando 100 "" kg de sucata de aço quando a corrente é desligada e o aço é descartado. Sabendo que o cabo e o guindaste de suporte têm uma rigidez total