Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 77

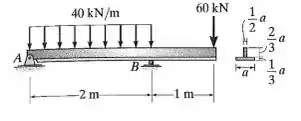
A viga está sujeita ao carregamento mostrado na figura. Determine a dimensão a exigida para sua seção transversal se a tensão admissível para o material for σmáx = 150 MPa.

Passo 1

Vamos, primeiramente, calcular as reações de apoio:

∑ M a = 0 → - 80 × 1 - 60 × 3 + 2 F b = 0

F b = 130 k N

∑ F y = 0 → F a + 130 - 80 - 60 = 0

F a = 10 k N

Agora, vamos fazer o diagrama de momento fletor para ver como o momento varia:

Como podemos ver, o momento máximo vale 60kNm.

Passo 2

Vamos determinar o momento de inércia e o centróide da seção da viga:

y c g = ∑ A y c g ∑ A = = a 3 × a a 6 + 2 a 3 × a 2 2 a 3 a 3 × a + 2 a 3 × a 2 = 5 a 12

I = a 12 a 3 3 + a × a 3 5 a 12 - a 6 2 + a 24 2 a 3 3 + a 2 × 2 a 3 2 a 3 - 5 a 12 2 = 37 a 4 648

Passo 3

A tensão é dada por:

σ m á x = M c I

Isolando-se o a , temos:

a = ( 60 × 10 3 × 7 × 648 3 ) 150 × 10 6 × 12 × 37 3 = 0,15988 m = 159,88   c m

Resposta

a = 159,88   c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

65. Determine a velocidade do centro O da bobina quando o cabo é puxado para a direita com uma velocidade v. A bobina rola sem deslizar.
68. Se a barra AB tem uma velocidade angular AB=4 rad/s, determine a velocidade do bloco deslizante C no instante mostrado.
67. A bicicleta tem uma velocidade v = 1,2 m/s e, no mesmo instante, a roda de trás tem uma velocidade angular no sentido horário ω = 3r a d / s , o que faz com que ela deslize em seu ponto de contato
66. Determine a velocidade do ponto A na borda exterior da bobina no instante mostrado quando o cabo é puxado para a direita com uma velocidade v. A bobina rola sem deslizar.
60. Determine a velocidade do ponto A na borda da engrenagem no instante mostrado.