Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 107

 16.107.  A placa quadrada está restringida dentro das ranhuras A E B . Quando θ = 30°, o ponto A está se deslocando com V A = 8 m / s . Determine a velocidade do ponto D.

Passo 1

Primeiro passo é encontrarmos o segmento de linha do ponto A , para isso e com base na geometria apresentada a baixo, podemos determinar que r A / I C com relação do ponto fixo I C perpendicular ao ponto.

r A /   I C =   0,3   cos ⁡ 30 °  

r A /   I C =   0,2598   m

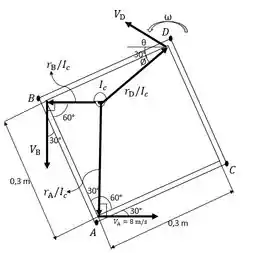
Passo 2

Velocidade angular do objeto será obtida pela relação entre a velocidade angular partindo do ponto A , no qual irá movimentar o objeto, e de seu respectivo segmento de linha:

ω = 8 0,2598 =

ω =   30,792   r a d / s

Passo 3

o segmento de linha do ponto B e D , para isso e com base na geometria apresentada podemos determinar que r B / I C com relação do ponto fixo I C perpendicular ao ponto.

r B /   I C = r B   s e n   30 °

r B /   I C =   0,3   s e n   30 ° =

r B /   I C =   0,15   m

Portanto...

r D /   I C   = ( r D ) 2 + ( r B / I C ) 2 - 2 r D r B / I C cos ⁡ 30 ° =

  r D /   I C   = ( 0,3 ) 2 + ( 0,15 ) 2 - 2 0,3 0,15 cos ⁡ 30 ° =

r D /   I C   =   0,1859   m

Passo 4

Tendo o segmento de linha do ponto D e a velocidade angular do objeto, podemos então determinarmos a velocidade deste ponto:

V D = r D /   I C . ω

V D   =   ( 0,1859 )   .   ( 30,792 )

V D =   5,72   m / s

Passo 5

Para determinarmos os ângulos podemos aplicar a lei dos senos, logo:

s e n   ϕ 0,15 = s e n   30 ° 0,1859

ϕ =   23,794 °

θ =     90 °   -   23,794 °   -   30 °

θ =   36,2 °

Resposta

V D =   5,72   m / s

θ =   36,2 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No projeto de uma planta de processamento de produção, uma cuba móvel com produtos está oscilando sob água pulverizada através da ação da barra de conexão AB da manivela OB. Para o instante em que θ =
Determine a velocidade angular ω da haste telescópica AB no instante representado. A velocidade angular de cada uma das barras de acionamento direto é indicada.
O volante gira no sentido horário com uma velocidade constante de 600 rpm, e a barra AB desliza através do cursor articulado em C. Para a posição θ=45 ° , determina a velocidade angular ω A B de AB ut
Os componentes de um dispositivo de comutação são mostrados. Se a haste de controle vertical tem uma velocidade descendente v = 0,9 m / s quando θ = 60 ° e se o cilindro A está em contato com a superf
No mecanismo de quatro barras mostrado, a haste de controle AO possui uma velocidade angular no sentido anti-horário ω O = 10 r a d / s durante um curto intervalo de movimento. Quando a haste CB ultra