Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 60

15.60. Uma cremalheira reta repousa sobre uma engrenagem de raio r 75 mm e está presa ao bloco B como mostra a figura. Sabendo que nesse instante a velocidade angular da engrenagem D é de 15 rpm no sentido anti-horário e 20°, determine (a) a velocidade do bloco B, (b) a velocidade angular da cremalheira.

Passo 1

Beleza, hora de resolver essa questão!

Vamos começar fazendo os cálculos mais simples. O enunciado nos dá

ω D = 15   r p m

Se colocarmos no SI

ω D = 15 ⋅ 2 π 60 = 0,5 π r a d s

Então podemos calcular a velocidade de um dente da engrenagem D .

v E = r ⋅ ω D = 0,075 ⋅ 0,5 π = 0,11781 m s

A gente pode calcular a distancia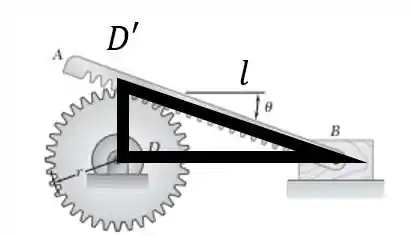 l entre D ' e B.

l = r tan ⁡ θ = 0,075 tan ⁡ 20 ° = 0,20606   m

Passo 2

Podemos fazer agora

E desenhando o diagrama de velocidades

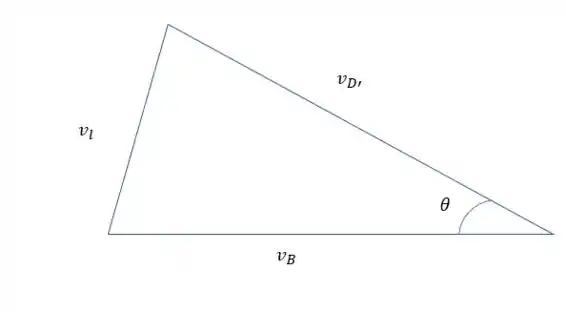
Nesse triangulo podemos ver as relações

v B = v D ' cos ⁡ θ

Então

v B = 0,11781 cos ⁡ 20 ° = 0,1254 m s

E essa é a resposta do item (a).

E também podemos tirar a relação

v l = v D ' tan ⁡ θ

Logo

v l = 0,11781 ⋅ tan ⁡ 20 ° = 0,4288 m s

Passo 3

Bom, agora vamos definir a velocidade angular da cremalheira. De acordo com a imagem temos:

l ω A B = v l

Então

ω A B = v l l = 0,04288 0,20606 = 0,208 r a d s

Resposta

a : v B = 0,1254 m s b :   ω A B = 0,208 r a d s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16.101. Se a barra A B está girando com uma velocidade angular A B = 3 r a d / s , determine a velocidade angular da barra C D no instante mostrado.
16.103. O mecanismo utilizado em um motor de navio consiste de uma manivela A B e duas bielas, B C E B D . Determine a velocidade do pistão em D no instante em que a manivela está na posição mostrada
16.108. O mecanismo produz movimento intermitente do segmento A B . Se a roda dentada S está girando com uma velocidade angular de ω S = 6 r a d / s , determine a velocidade angular do segmento A B ne
16.102. O mecanismo utilizado em um motor de navio consiste de uma manivela A B e duas bielas, B C E B D . Determine a velocidade do pistão em C no instante em que a manivela está na posição mostrada
16.100. Se a barra A B está girando com uma velocidade angular A B = 3 r a d / s , determine a velocidade angular da barra B C no instante mostrado.