Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 100
16.100. Se a barra está girando com uma velocidade angular = , determine a velocidade angular da barra no instante mostrado.
Passo 1
Diagrama Cinemático: A partir da geometria =
Como as barras e estão girando em torno dos pontos fixos e , o e o são sempre direcionados perpendicularmente as barras e, respectivamente.
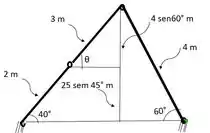
Fig. a
= .
= . =
No instante mostrado, o é direcionado em um ângulo de enquanto o é direcionado a
Passo 2
Centro instantâneo: O centro instantâneo de velocidade zero da barra no instante mostrado está localizado no ponto de interseção de linhas estendidas desenhadas perpendicularmente ao e . Usando a lei dos senos, temos:
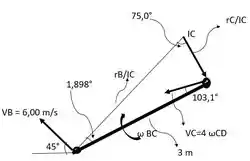
Fig.b
= =
=
Passo 3
Logo o segmento de linha para o ponto será atribuindo a mesma lógica.
= =
=
Passo 4
A velocidade angular da barra é dada pela relação entre a velocidade linear em e seu respectivo segmento de linha.
= = =
Resposta
=