16.108. O mecanismo produz movimento intermitente do segmento A B . Se a roda dentada S está girando com uma velocidade angular de ω S = 6 r a d / s , determine a velocidade angular do segmento A B nesse instante. A roda dentada S está montada em um eixo, o qual é separado de outro eixo colinear fixado a A B em A . O pino C está fixado a um dos elos da corrente.

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 108

16.108. O mecanismo produz movimento intermitente do segmento . Se a roda dentada está girando com uma velocidade angular de = 6 determine a velocidade angular do segmento nesse instante. A roda dentada está montada em um eixo, o qual é separado de outro eixo colinear fixado a em . O pino está fixado a um dos elos da corrente.

Passo 1

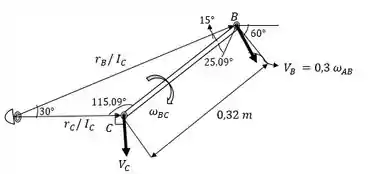
Diagrama cinemático: Como o link AB está girando em torno do ponto fixo A, o vB é sempre direcionado perpendicularmente ao link AB e sua magnitude é = . No instante mostrado é direcionado em um ângulo de com a horizontal. Como o ponto está preso à corrente, no instante mostrado, ele se move verticalmente com uma velocidade de:

= = 6(0,175) = 1,05

Passo 2

Centro instantâneo: O centro instantâneo de velocidade zero do eixo no instante mostrado está localizado no ponto de interseção de linhas estendidas desenhadas perpendicularmente a e. Usando a lei dos senos, temos:

Portanto,

Passo 3

A velocidade angular da barra BC é dada pela relação entre a velocidade linear em C e do seu respectivo segmento, pois através do ponto fixo em na corrente, transmitirá o movimento para a engrenagem:

= =

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/110) A roda motriz traseira de um automóvel tem um diâmetro de 650m m e tem uma velocidade angular N de 200r p m em uma estrada coberta de gelo . Se o centro instantâneo de velocidade nula está 100m

5/94) A barra com restrições do Prob.5/81 é reapresentada aqui . A extremidade A da barra possui uma velocidade descendente v A de 2 m / s durante um intervalo de seu movimento . Para a posição onde θ

5/96) Para o instante representado , quando a manivela O A passa pela posição horizontal , determine a velocidade do centro G da barra A B pelo método dessa seção .

5/107) Ocorpo retangular B é articulado à manivela O A em A e é apoiado pela roda em D . Se O A possui uma velocidade angular no sentido anti-horário de 2r a d / s , determine a velocidade do ponto E

5/101) O mecanismo do Prob.5/27 é reapresentado aqui. No instante em que x A = 0,85 L , a velocidade do cursor em A é v = 2 m / s para a direita . Determine a velocidade correspondente do cursor B e a