Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 92
16.92. Se a extremidade do cabo é puxada para baixo com uma velocidade = 4 , determine a velocidade angular da bobina e a velocidade do ponto localizado na borda exterior da bobina.
Passo 1
Movimento geral do plano: Como o ponto de contato, o cabo e a bobina estão em repouso, o está localizado no ponto A partir da geometria da Fig. a.
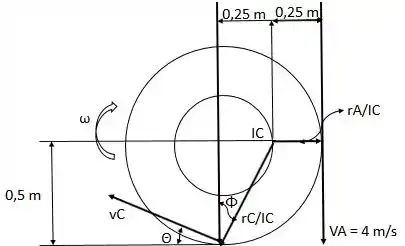
Fig. a
Passo 2
Com relação a fig.a, podemos determinar o valor imediato da intersecção do segmento de linha , e para teremos que medir a distância entre os dois pontos e , portanto:
= =
= 0,5590
Podemos também usar a tangente inversa para encontrar o ângulo :
Passo 3
Assim, a velocidade angular do carretel pode ser determinada a partir da relação entre a velocidade do segmento e da intersecção do segmento de linha.
=
Passo 4
Determinado o valor da velocidade angular, podemos inseri-la na equação onde iremos relacioná-la com da intersecção do segmento de linha para achar a velocidade linear no segmento
=
Passo 5
E sua direção será , logo sabemos que:
Resposta
= 16
8,94