Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 97
16.97. A unidade de bombeamento de petróleo consiste de um balancim , a barra de conexão e a manivela Se a manivela gira com uma taxa constante de 6 determine a velocidade da barra no instante mostrado. Dica: O ponto segue uma trajetória circular em torno do ponto e portanto, a velocidade de não é vertical.
Passo 1
Diagrama Cinemático: Da geometria = 9,462° e = = 2,737 Como o da manivela e a viga são rotativos em torno dos pontos fixos e , o e são sempre direcionados perpendicularmente ao da manivela
e do feixe , respectivamente. A magnitude do e são :
= . = 6.(0,9) = 5,4 ,
= 6.(0,9) =
= 5,4
Logo...
= . = 2,737 .
= 2,737 .
No instante mostrado, o é direcionado verticalmente, enquanto o é direcionado com um ângulo de 9,462° na vertical.
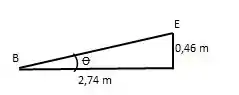
Fig. a
Passo 2
Centro instantâneo: O centro instantâneo de velocidade zero da barra no instante mostrado, localizado no ponto de interseção de linhas estendidas traçadas perpendiculares a e . Da geometria a seguir:
/ =
/ = =
/ =
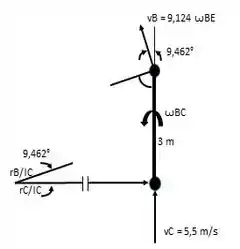
Fig. b
Passo 3
Podemos definir o segmento de linha em a partir da relação entre a distância dos pontos e o ângulo formado na haste:
/ = =
/ = 18,00
Passo 4
A velocidade angular da barra é dada pela seguinte equação, na qual usaremos a velocidade e o segmento de linha no ponto .
= =
= =
= 0,3
Passo 5
Assim, a velocidade angular do feixe é dada pelos segmentos dependentes, ou seja, a velocidade angular da barra e o segmento de linha do ponto :
= .
2,737= 0,3 . (18,25) =
= 2,00
Passo 6
Logo, concluiremos que, a velocidade da haste é dada pela relação entre a velocidade angular dos pontos e da distância entre :
= . = 2,00 . (2,7) = 5,4
= 2,00 . (2,7) =
= 5,4
Resposta
= 5,4