Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 71
As rodas A e B têm uma massa de 75 kg e 50 kg, respectivamente. Inicialmentem a roda A gira no sentido horário com uma velocidade angular constante de = 100 rad/s e a roda B está em repouso. Se A é colocada em contato com B, determine o tempo requerido para ambas as rodas alcançarem a mesma velocidade angular. O coeficiente de atrito cinético entre as duas rodas é = 0,3 e os raios de giração de A e B em relação aos seus centos de massa respectivos são = 0,3 m e = 0,225 m. Despreze o peso do membro AC.
Passo 1
Para resolver esse exercício, iremos considerar a aceleração da gravidade como .
Primeiro, devemos notar que enquanto as duas rodas não estiverem girando com a mesma velocidade angular, haverá força de atrito cinético entre elas, logo:
Podemos já calcular o momento de inércia das duas rodas. Para a roda A:
Para a roda B:
Passo 2
Tomaremos os seguintes diagramas de corpo livre para aplicar as equações de movimento. Roda A:
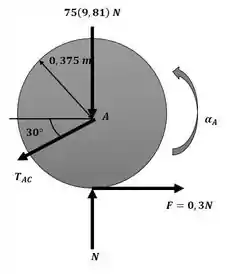
Roda B:
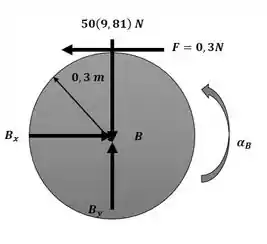
No passo 2 iremos aplicar as equações de movimento para as rodas A e B para descobrir as forças atuantes e a aceleração angular de cada uma delas.
Para a roda A:
Essa será nossa equação número 1.
Essa será nossa equação número 2.
Essa será nossa equação número 3.
Isolando N da equação número 2 e substituindo na equação número 3:
Substituindo esse valor na equação 2:
E, para descobrir a aceleração usaremos esse valor na equação número 1:
Agora, iremos aplicar o somatório de momento em torno do ponto B para descobrir a aceleração angular de B:
Passo 3
Agora, com o valores da acelerações angulares, podemos aplicar as equações da velocidade para A e B, obteremos expressões em função do tempo.
Para a roda A:
Para a roda A:
Como queremos que as rodas tenham a mesma velocidade angular, iremos igualar e e obter o tempo necessário para que isso ocorra: