Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 222

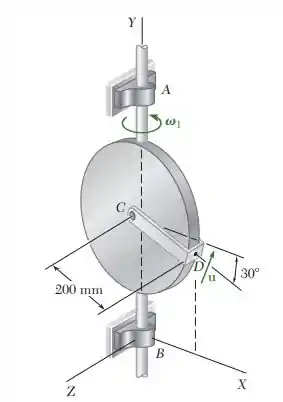
15.222. A placa circular mostrada na figura gira em torno de seu diâmetro vertical a uma taxa constante 1 10 rad /s. Sabendo que na posição mostrada o disco se encontra no plano XY e o ponto D da alça CD se desloca para cima com velocidade relativa u 1,5 m/s, determine (a) a velocidade de D, (b) a aceleração de D

Passo 1

Vamos começar já escrevendo um vetor: r → D C .

Pela geometria da figura podemos definir

r → D C = 0,2 cos ⁡ 30 °   i ^ - sin ⁡ 30 °   j ^

Ou seja

r → D C = 0,1 3   i ^ - 0,1 j ^ m

E pelo referencial que estamos usando também podemos definir

Ω → = ω 1   j ^ = 10   j ^ r a d s

Passo 2

Agora vamos começar os cálculos! A velocidade pode ser calculada assim:

v → D = v → D ' + v → D F

Vamos resolver termo por termo.

v → D ' = Ω → × r → D C

Olha só, no passo anterior a gente já calculou tudo isso.

v → D ' = 10   j ^ × 0,1 3   i ^ - 0,1 j ^

Isso fica

v → D ' = - 3   k ^ m s  

E agora o segundo termo

v → D F = u → sin ⁡ 30 °   i ^ + cos ⁡   30 °   j ^

Então

v → D F = 0,75   i ^ + 0,75   3   j ^ m s

Então a resposta do item (a) fica

v → D = 0,75   i ^ + 0,75   3   j ^ - 3   k ^ m s

Ou então

Passo 3 v → D = 0,75   i ^ + 1299   j ^ - 1732   k ^ m s

Passo 3

Agora vamos para o item (b). Para calcular a aceleração podemos usar

a → D = a → D ' + a → D F + 2 Ω × v → D F

Vamos fazer novamente por termos.

a → D ' = - Ω 2 r c o s   30 °   i ^

Então

a → D ' = - 10 2 0,1 3 i ^ = - 10 3   i ^ m s 2

Agora o segundo termo

a → D F = u 2 ρ ⋅ - cos ⁡ 30 °   i ^ + sin ⁡ 30 °   j ^

Isso fica

a → D F = 1,5 2 0,2 ⋅ - cos ⁡ 30 °   i ^ + sin ⁡ 30 °   j ^

a → D F = - 5,625 3   i ^ + 5,625   j ^ m s 2

E o último termo, a aceleração de Coriolis.

2 Ω × v → D F = 2 10 j ^ × 0,75   i ^ + 0,75   3   j ^

Isso fica

2 Ω × v → D F = - 15   k ^ m s 2

Então

a → D = 10 3 - 5,625 3   i ^ + 5,625   j ^ - 15   k ^ m s 2

Ou

a → D = 27,1   i ^ + 5,6 3   j ^ - 15   k ^ m s 2

Resposta

a : v → D = 0,75   i ^ + 1299   j ^ - 1732   k ^ m s b :   a → D = 27,1   i ^ + 5,63   j ^ - 15   k ^ m s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O corpo AB e a haste BC do componente robótico mostrado giram a uma taxa constante ω 1 = 0.60 r a d / s em torno do eixo Y. Simultaneamente, um controle de arame e polia faz com que o braço CD gire em
A manivela AB tem uma velocidade angular constante de 1,5 rad/s gira no sentido anti-horário. Para a posição mostrada, determine (a) a velocidade angular da haste BD, (b) a velocidade do colar D.
Sabendo que no instante mostrado a barra AB tem aceleração angular nula e velocidade angular de 15r a d / s no sentido anti-horário, determine (a) a aceleração angular do braço D E , (b) a aceleração
O colar P desliza para fora a uma velocidade relativa constante u ao longo da barra AB, que gira no sentido anti-horário com uma velocidade angular constante de 20r p m . Sabendo que r = 250m m quando
O pino P desliza em uma ranhura circular cortada na placa mostrada na figura com uma velocidade relativa constante u = 90m m / s . Sabendo que, no instante mostrado, a velocidade angular ω da placa é