Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas fundamentais - Ex. 16
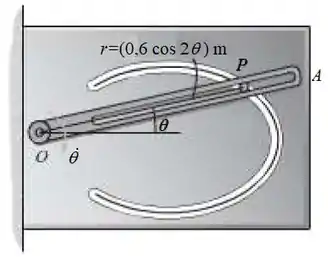
O pino de 0,2 kg está restrito a se mover na fenda curva lisa que é definida pela lemniscata m. O seu movimento é controlado pela rotação do braço bifurcado , o qual tem velocidade angular constante no sentido horário de rad/s. Determine a força que o braço exerce sobre o pino quando . O movimento está no plano vertical.
Passo 1
O enunciado nos dá as seguintes informações:
Massa do pino :
Velocidade angular constante:
A questão pede para determinarmos a força que o braço exerce sobre o pino quando
Vamos considerar esse problema como bidimensional. Desenhamos o diagrama de corpo livre do pino na posição
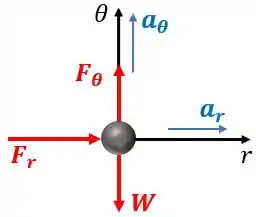
Onde é a força peso e .
Podemos ver que a força exercidada pela barra no momento em que é igual . Logo,
Passo 2
Primeiramente, vamos encontrar as derivadas temporais do pino em ( e ):
Sabemos que , portanto
Agora vamos substituir o valor de pelo instante pedido. Neste cálculo, devemos tomar cuidado pois deve estar em radiano.
No instante rad, teremos
Passo 3
Sabemos que as componentes da aceleração do pino nas coordenadas e são dadas por
Logo,
Passo 4
Agora aplicaremos as Equações do Movimento.
Como a questão só nos pede valor de , analisaremos apenas o eixo .