Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 35

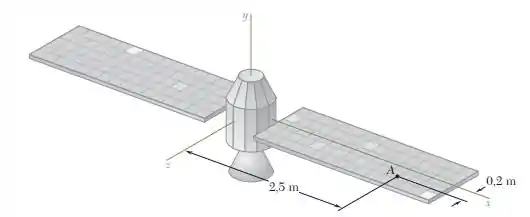
18.35. Os eixos de coordenadas mostrados na figura representam os eixos centroidais principais de inércia de uma sonda espacial de 1.500 kg cujos raios de giração são kx 0,4 m, ky 0,45 m e kz 0,375 m. A sonda não tem velocidade angular quando um meteorito de 150 g atinge um de seus painéis solares em A com uma velocidade v0 (720 m/s)i (900 m/s)j (960 m/s)k em relação à sonda. Sabendo que o meteorito emerge do outro lado do painel sem mudança na direção de sua velocidade, mas com uma redução de 20% na sua intensidade, determine a velocidade angular final da sonda.

Passo 1

Então temos a seguinte situação: uma sonda que estava parada de boa no espaço é atingida por um meteorito. O meteorito atinge a sonda com a velocidade:

v → 0 = 720   i ^ - 900   j ^ + 960   k ^ m s

No ponto A:

r → A = 2,5   i ^ + 0,2   k ^ m s  

Passo 2

Agora podemos começar a calcular! Temos um problema de momento aqui, então o melhor que fazemos agora é calcular os momentos iniciais. O momento linear inicial do meteorito é:

L → i = m v → 0 = 0,150 ⋅ 720   i ^ - 900   j ^ + 960   k ^

Então

L → i = 108   i ^ - 135   j ^ + 144   k ^   k g   m s 2

E o momento angular em relação a origem é|

H → A i = r → A × m v → 0

Isso fica

H → A i = i ^ j ^ k ^ 2,5 0 0,2 108 - 135 144

Então

H → M i = 0 + 27 i ^ + 21,6 - 360 j ^ + - 337,5 k ^

Ou seja

H → M i = 27   i ^ - 338,4   j ^ - 337,5   k ^   k g m 2 s

E agora vamos calcular os momentos finais. Isso aqui não vai ser difícil porque sabemos que nada mudou, exceto a velocidade, esta diminui em 20 % , ou seja, a velocidade final é 80 % da velocidade inicial:

v = 0,8 v 0

Então temos

L → f = m 0,8 v 0 = 0,8 ⋅ 108   i ^ - 135   j ^ + 144   k ^  

Isso fica

L → f = 86,4   i ^ - 108   j ^ + 115,2   k ^   k g   m s 2

E o momento angular final

H → M f = r → A × 0,8 m v → 0 = 0,8 27   i ^ - 338,4   j ^ - 337,5   k ^  

Então

H → M f = 21,6   i ^ - 270,72   j ^ - 270   k ^   k g m 2 s

Passo 3

Vamos focar na sonda agora, podemos considerar que inicialmente seu momento angular é:

H → A i = I x ω x   i ^ + I y ω y   j ^ + I z ω z   k ^

Ou então

H → A i = ω x ⋅ M k x 2   i ^ + ω y ⋅ M k y 2 j ^ + ω z ⋅ M k z 2   k ^

Substituindo os valores:

H → A i = 1500 ω x ⋅ 0,4 2   i ^ + ω y ⋅ 0,45 2   j ^ + ω z ⋅ 0,375 2   k ^

Isso fica

H → A = ω x 240   i ^ + ω y 303,75   j ^ + ω z 210,9375   k ^   k g m 2 s

Mas para o sistema sonda-meteorito podemos considerar que

H → M i = H → A i + H M f

Ou

H → A i = H → M i - H → M f

Agora só substituir os valores

ω x 240   i ^ + ω y 303,75   j ^ + ω z 210,9375   k ^ = 27   i ^ - 338,4   j ^ - 337,5   k ^ - 21,6   i ^ - 270,72   j ^ - 270   k ^  

Isso fica

ω x 240   i ^ + ω y 303,75   j ^ + ω z 210,9375   k ^ = 5 , 4   i ^ - 67,68   j ^ - 67,5   k ^

Agora resolvendo para cada componente temos:

ω x = 5,4 240 = 0,0225 r a d s

ω y = - 67,68 303,75 = - 0,2228 r a d s

ω z = - 67,5 210,9375 = - 0,32 r a d s

Então a resposta pro nosso problema é

ω → = 0,0225   i ^ - 0,2228   j ^ - 0,32   k ^ r a d s

Resposta

ω → = 0,0225   i ^ - 0,2228   j ^ - 0,32   k ^ r a d s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O conjunto mostrado na figura tem massa de 6 kg e consiste em quatro placas finas semicirculares de alumínio com 400 mm de diâmetro, soldadas a um eixo leve AB de 1 m de comprimento. O conjunto está e
SAbendo que o conjunto do Problema 18.65 está inicialmente em repouso ( ω = 0) quando um binário de momento M0 = (0,75 N ∙ m)j é aplicado ao eixo, determine (a) a aceleração angular resultante do conj
SAbendo que o conjunto do Problema 18.65 está inicialmente em repouso ( ω = 0) quando um binário de momento M0 = (0,75 N ∙ m)j é aplicado ao eixo, determine (a) a aceleração angular resultante do conj
Uma haste delgada é dobrada para formar uma moldura quadrada de lado 6 pol. A moldura é fixada por um colar em A a um eixo vertical que gira com uma velocidade angular constante ω. Determine o valor d
As pás de um ventilador oscilante e o rotor de seu motor têm massa total de 250 g e um raio de giração combinado de 75 mm. Eles estão apoiados em mancais em A e B, distantes de 125 mm, e giram à taxa