Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 51

Determine a energia cinética perdida quando a placa do Problema 18.29 bate na obstrução no ponto B.

Passo 1

Vamos lá resolver mais essa. Definindo um sistema de eixos, como mostrado na figura, a velocidade angular inicial tem as seguintes componentes

ω x ' = 2 2 ω 0 ,   ω y ' = 2 2 ω 0

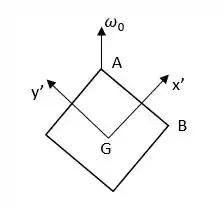
A quantidade de movimento angular inicial sobre o centro de massa é:

H → G 0 = I - x ' ω x ' i → + I - y ' ω y ' j → = 1 12 m a 2 2 2 ω 0 i ' → + j ' →

Sendo que a velocidade inicial do centro de massa é v → 0 = 0

Vamos considerar que ω → e v → são a velocidade angular e a velocidade do centro de massa imediatamente após o impacto. A velocidade do ponto B é

v → B = ω → × r → B / A = ω x ' i ' → + ω y ' j → + ω z ' k ' → × - a j ' →

v → B = a ω z ' i ' → + ω x ' k ' →

Como o impacto é perfeitamente plástico, v B z ' = 0 ou ω x ' = 0 . Logo a velocidade do centro de massa é:

v → = ω → × r → G / A = ω y ' j ' → + ω z ' k → × 1 2 a 9 - - i ' → - j ' → = 1 2 a ω z ' i ' → - ω z ' j ' → + ω y ' k ' →

Além disso, o momento angular de A em relação a G é:

r → G / A × m v → = 1 4 m a 2 - ω y ' i ' → + ω y ' j ' → + 2 ω z ' k ' →

A quantidade de movimento do centro de massa é:

H G = I x ' ω x ' i ' → + I y ' ω y ' j ' → + I z ' ω z ' k ' → = 1 12 m a 2 ω y ' j ' → + 1 6 m a 2 ω z ' k ' →

Passo 2

Agora vamos utilizar o princípio de impulso e quantidade de movimento para calcular a velocidade angular e a velocidade do centro de massa. O impulso do impacto em B é F Δ t k → . Assim, temos que

H → A 0 + - a j → × F Δ t k → = H → A

H → G 0 + r → G / A × m v → 0 - a F Δ t i → = H → G + r → G / A × m v →

2 24 m a 2 ω 0 i ' → + j ' → - a F Δ t i → = 1 12 m a 2 ω y ' j ' → + 1 6 m a 2 ω z ' k ' → + 1 4 m a 2 - ω y ' i ' → + ω y ' j ' → + 2 ω z ' k ' →

Resolvendo em relação aos componentes auxiliares:

1 24 2 m a 2 ω 0 = 1 12 m a 2 ω y ' + 1 4 m a 2 ω y '

ω y ' = 2 8 ω 0

0 = 1 6 m a 2 ω z ' + 1 2 m a 2 ω z '

ω z ' = 0

Como j ' → = - 2 2 i → + 2 2 j → , temos que

ω → = 2 8 ω 0 j ' → = 1 8 2 ω 0 2 2 - i → + j →

ω → = 1 8 ω 0 - i → + j →

v → = 1 2 a ω y ' k ' → = 2 16 a ω 0 k →

Passo 3

A energia cinética é dada por:

T = 1 2 m v - 2 + 1 2 I - x ω x ' 2 + 1 2 I - y ω y ' 2 + 1 2 I - z ω z ' 2

Antes do impacto, temos que v - 0 = 0 , ω x ' = 2 2 ω 0 e ,   ω y ' = 2 2 ω 0 . A energia cinética nesse instante é:

T 0 = 0 + 1 2 1 12 m a 2 2 2 ω 0 2 + 1 2 1 12 m a 2 2 2 ω 0 2 + 0 = 1 24 m a 2 ω 0 2

Após o impacto, v - =   2 16 a ω 0 e ω y ' = 2 8 ω 0 . Assim,

T 1 = 1 2 m 2 16 a ω 0 2 + 0 + 1 2 1 12 m a 2 2 8 ω 0 + 0 = 1 192 m a 2 ω 0 2

Logo, a energia cinética perdida é:

T 0 - T 1 = 1 24 m a 2 ω 0 2 - 1 192 m a 2 ω 0 2 = 7 192 m a 2 ω 0 2

Resposta

T 0 - T 1 = 7 192 m a 2 ω 0 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

18.45. Determine a energia cinética do corpo do Problema 18.19.
18.44. Determine a energia cinética da placa triangular do Problema 18.16
18.35. Os eixos de coordenadas mostrados na figura representam os eixos centroidais principais de inércia de uma sonda espacial de 1.500 kg cujos raios de giração são kx 0,4 m, ky 0,45 m e kz 0,375 m.
18.36. Os eixos de coordenadas mostrados na figura representam os eixos centroidais principais de inércia de uma sonda espacial de 1.500 kg cujos raios de giração são kx 0,4 m, ky 0,45 m e kz 0,375 m.
18.34. Resolva o Problema 18.33 considerando que a velocidade angular da sonda seja (0,060 rad /s)i (0,040 rad /s)k.